Question Number 23012 by A1B1C1D1 last updated on 25/Oct/17
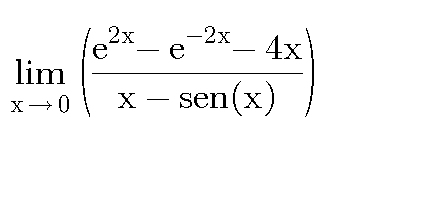
Commented by ajfour last updated on 25/Oct/17
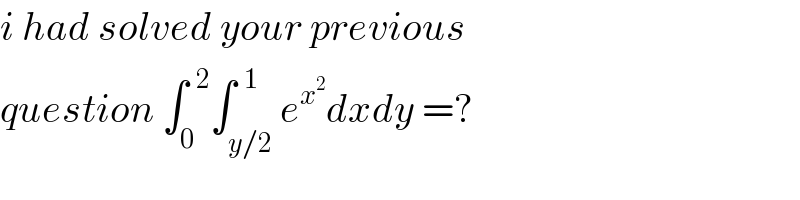
$${i}\:{had}\:{solved}\:{your}\:{previous}\: \\ $$$${question}\:\int_{\mathrm{0}} ^{\:\:\mathrm{2}} \int_{{y}/\mathrm{2}} ^{\:\:\mathrm{1}} {e}^{{x}^{\mathrm{2}} } {dxdy}\:=? \\ $$
Commented by A1B1C1D1 last updated on 25/Oct/17

$$\mathrm{Yes}! \\ $$
Answered by ajfour last updated on 25/Oct/17
![=lim_(x→0) ((([1+2x+((4x^2 )/(2!))+((8x^3 )/(3!))+]..−[1−2x+((4x^2 )/(2!))−((8x^3 )/(3!))]−4x)/(x−x+(x^3 /(3!))−...))) =lim_(x→0) (((2×((8x^3 )/(3!))+...)/((x^3 /(3!))+....))) = 16 .](https://www.tinkutara.com/question/Q23015.png)
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\left[\mathrm{1}+\mathrm{2}{x}+\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{3}!}+\right]..−\left[\mathrm{1}−\mathrm{2}{x}+\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}!}−\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{3}!}\right]−\mathrm{4}{x}}{{x}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−…}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2}×\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{3}!}+…}{\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+….}\right)\:=\:\mathrm{16}\:. \\ $$
Commented by A1B1C1D1 last updated on 26/Oct/17

$$\mathrm{Thank}\:\mathrm{you}. \\ $$
Commented by A1B1C1D1 last updated on 26/Oct/17

$$\mathrm{You}\:\mathrm{did}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sine}\:\mathrm{function}\:\mathrm{in}\:\mathrm{infinite}\:\mathrm{series},\:\mathrm{right}?\: \\ $$
Answered by FilupS last updated on 26/Oct/17
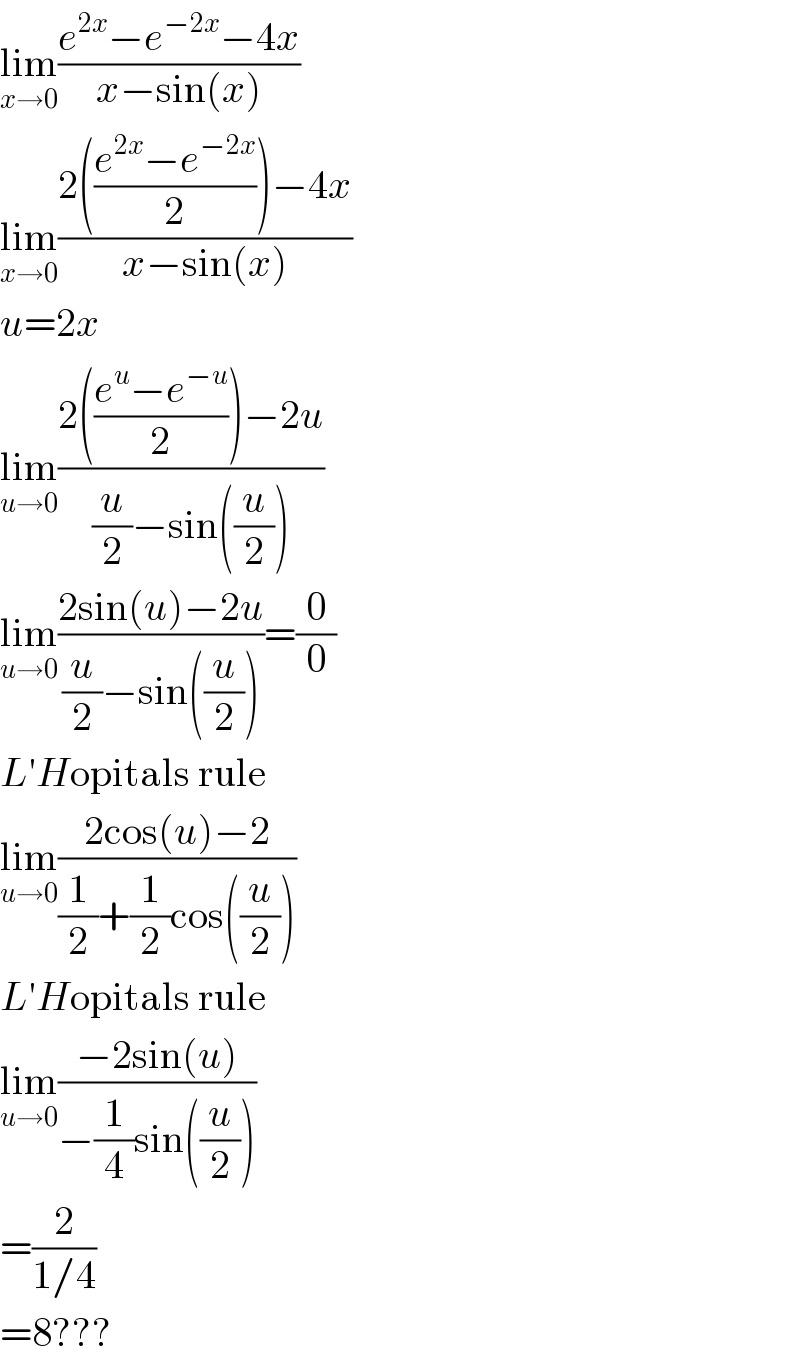
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\mathrm{2}{x}} −{e}^{−\mathrm{2}{x}} −\mathrm{4}{x}}{{x}−\mathrm{sin}\left({x}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left(\frac{{e}^{\mathrm{2}{x}} −{e}^{−\mathrm{2}{x}} }{\mathrm{2}}\right)−\mathrm{4}{x}}{{x}−\mathrm{sin}\left({x}\right)} \\ $$$${u}=\mathrm{2}{x} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left(\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}}\right)−\mathrm{2}{u}}{\frac{{u}}{\mathrm{2}}−\mathrm{sin}\left(\frac{{u}}{\mathrm{2}}\right)} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\left({u}\right)−\mathrm{2}{u}}{\frac{{u}}{\mathrm{2}}−\mathrm{sin}\left(\frac{{u}}{\mathrm{2}}\right)}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$${L}'{H}\mathrm{opitals}\:\mathrm{rule} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2cos}\left({u}\right)−\mathrm{2}}{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\frac{{u}}{\mathrm{2}}\right)} \\ $$$${L}'{H}\mathrm{opitals}\:\mathrm{rule} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\left({u}\right)}{−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\frac{{u}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}/\mathrm{4}} \\ $$$$=\mathrm{8}??? \\ $$
Commented by A1B1C1D1 last updated on 26/Oct/17

$$\mathrm{16}… \\ $$
Commented by FilupS last updated on 26/Oct/17
$$\mathrm{I}\:\mathrm{cant}\:\mathrm{find}\:\mathrm{my}\:\mathrm{mistake} \\ $$
Commented by A1B1C1D1 last updated on 26/Oct/17
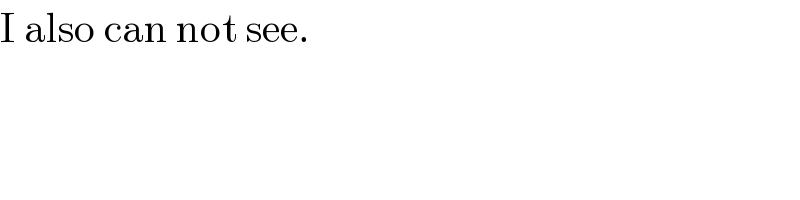
$$\mathrm{I}\:\mathrm{also}\:\mathrm{can}\:\mathrm{not}\:\mathrm{see}. \\ $$
Commented by ajfour last updated on 26/Oct/17

$$\mathrm{sin}\:{u}\:{or}\:\mathrm{sinh}\:{u}\:? \\ $$
Commented by A1B1C1D1 last updated on 26/Oct/17
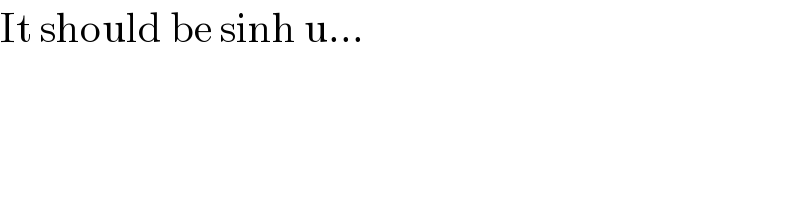
$$\mathrm{It}\:\mathrm{should}\:\mathrm{be}\:\mathrm{sinh}\:\mathrm{u}…\: \\ $$
