Question Number 23138 by math solver last updated on 26/Oct/17

Commented by math solver last updated on 26/Oct/17

$$\mathrm{q}.\mathrm{4}? \\ $$
Answered by ajfour last updated on 26/Oct/17
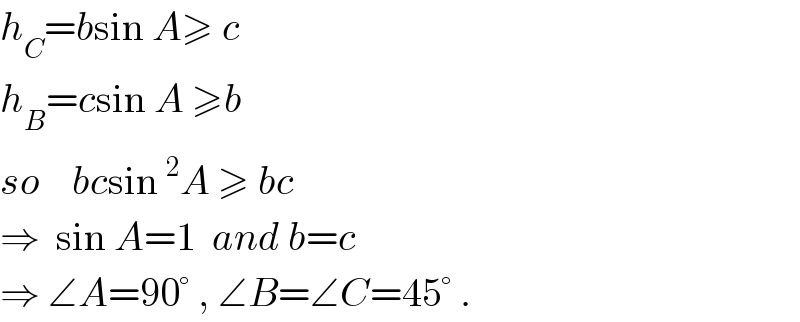
$${h}_{{C}} ={b}\mathrm{sin}\:{A}\geqslant\:{c} \\ $$$${h}_{{B}} ={c}\mathrm{sin}\:{A}\:\geqslant{b} \\ $$$${so}\:\:\:\:{bc}\mathrm{sin}\:^{\mathrm{2}} {A}\:\geqslant\:{bc} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:{A}=\mathrm{1}\:\:{and}\:{b}={c} \\ $$$$\Rightarrow\:\angle{A}=\mathrm{90}°\:,\:\angle{B}=\angle{C}=\mathrm{45}°\:. \\ $$
Commented by ajfour last updated on 26/Oct/17
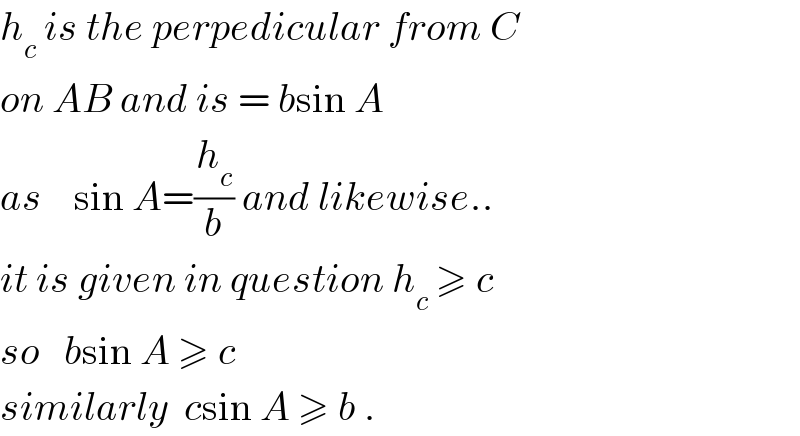
$${h}_{{c}} \:{is}\:{the}\:{perpedicular}\:{from}\:{C} \\ $$$${on}\:{AB}\:{and}\:{is}\:=\:{b}\mathrm{sin}\:{A} \\ $$$${as}\:\:\:\:\mathrm{sin}\:{A}=\frac{{h}_{{c}} }{{b}}\:{and}\:{likewise}.. \\ $$$${it}\:{is}\:{given}\:{in}\:{question}\:{h}_{{c}} \:\geqslant\:{c} \\ $$$${so}\:\:\:{b}\mathrm{sin}\:{A}\:\geqslant\:{c} \\ $$$${similarly}\:\:{c}\mathrm{sin}\:{A}\:\geqslant\:{b}\:. \\ $$
Commented by math solver last updated on 26/Oct/17
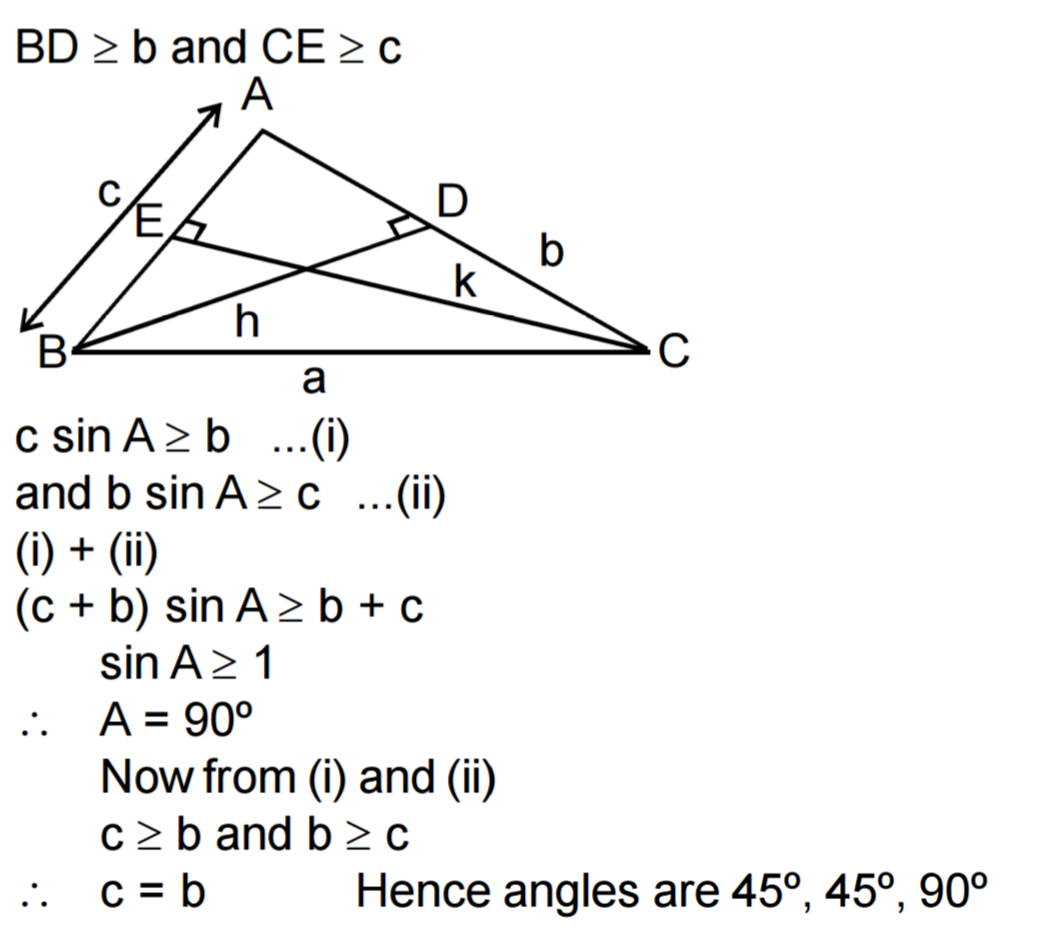
Commented by math solver last updated on 26/Oct/17

$$\mathrm{same}\:\mathrm{sol}.\:\mathrm{is}\:\mathrm{given}\:\mathrm{in}\:\mathrm{book}\:\mathrm{but}\: \\ $$$$\mathrm{i}\:\mathrm{could}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{1st}\:\mathrm{2}\: \\ $$$$\mathrm{lines}\:\mathrm{eq}.\:\mathrm{i}.\mathrm{e}\:\mathrm{h}\:_{\mathrm{c}} \:\mathrm{and}\:\mathrm{h}_{\mathrm{b}} \:? \\ $$
Commented by math solver last updated on 26/Oct/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:! \\ $$
