Question Number 23179 by Joel577 last updated on 27/Oct/17
Commented by Joel577 last updated on 27/Oct/17

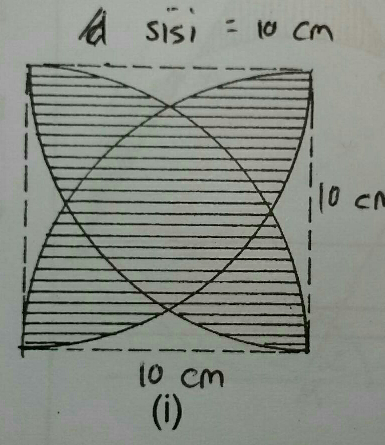
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{part} \\ $$
Answered by ajfour last updated on 27/Oct/17
![let 10cm=a eq. of circle with centre as top left corner is y=a−(√(a^2 −x^2 )) Area of bottom unshaded region =2∫_0 ^( a/2) [a−(√(a^2 −x^2 )) ]dx =2[ax−(x/2)(√(a^2 −x^2 ))−(a^2 /2)sin^(−1) ((x/a))]_0 ^(a/2) =2[(a^2 /2)−((a^2 (√3))/8)−((πa^2 )/(12))] Shaded area =a^2 −8[(a^2 /2)−((a^2 (√3))/8)−((πa^2 )/(12))] =−3a^2 +a^2 (√3)+((2π)/3)a^2 with a=10cm Shaded Area=100(((2π)/3)+(√3)−3)cm^2 ≈ 100(2.095+1.732−3)cm^2 ≈ 82.7 cm^2 .](https://www.tinkutara.com/question/Q23184.png)
$${let}\:\mathrm{10}{cm}={a} \\ $$$${eq}.\:{of}\:{circle}\:{with}\:{centre}\:{as}\:{top} \\ $$$${left}\:{corner}\:{is}\:\:{y}={a}−\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\: \\ $$$${Area}\:{of}\:{bottom}\:{unshaded} \\ $$$${region}\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\:{a}/\mathrm{2}} \left[{a}−\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\right]{dx} \\ $$$$=\mathrm{2}\left[{ax}−\frac{{x}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)\right]_{\mathrm{0}} ^{{a}/\mathrm{2}} \\ $$$$=\mathrm{2}\left[\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{8}}−\frac{\pi{a}^{\mathrm{2}} }{\mathrm{12}}\right] \\ $$$${Shaded}\:{area}\:={a}^{\mathrm{2}} −\mathrm{8}\left[\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{8}}−\frac{\pi{a}^{\mathrm{2}} }{\mathrm{12}}\right] \\ $$$$\:\:\:\:=−\mathrm{3}{a}^{\mathrm{2}} +{a}^{\mathrm{2}} \sqrt{\mathrm{3}}+\frac{\mathrm{2}\pi}{\mathrm{3}}{a}^{\mathrm{2}} \\ $$$${with}\:{a}=\mathrm{10}{cm} \\ $$$$\boldsymbol{{S}}{haded}\:\boldsymbol{{A}}{rea}=\mathrm{100}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\sqrt{\mathrm{3}}−\mathrm{3}\right){cm}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\approx\:\mathrm{100}\left(\mathrm{2}.\mathrm{095}+\mathrm{1}.\mathrm{732}−\mathrm{3}\right){cm}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\approx\:\mathrm{82}.\mathrm{7}\:{cm}^{\mathrm{2}} \:. \\ $$
Commented by Joel577 last updated on 27/Oct/17

$${I}\:{dont}\:{understand}\:{how}\:{can}\:{u}\:{get}\:{y}\:=\:{a}\:−\:\sqrt{{a}^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} } \\ $$
Commented by Rasheed.Sindhi last updated on 27/Oct/17

$$\mathrm{Can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{without}\:\mathrm{calculus}? \\ $$
Commented by Joel577 last updated on 27/Oct/17

$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by mrW1 last updated on 27/Oct/17

$$\mathrm{let}\:\mathrm{a}=\mathrm{10} \\ $$$$\mathrm{b}=\mathrm{2a}×\mathrm{sin}\:\frac{\mathrm{30}°}{\mathrm{2}}=\mathrm{2a}×\mathrm{sin}\:\mathrm{15}°=\mathrm{a}\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\mathrm{A}_{\mathrm{shade}} =\mathrm{8}×\frown+\mathrm{4}×\Delta+\mathrm{1}×\Box \\ $$$$=\mathrm{8}×\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{6}}−\mathrm{sin}\:\mathrm{30}^{°} \right)+\mathrm{4}×\frac{\mathrm{b}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}\mathrm{b}}{\mathrm{2}}+\mathrm{b}^{\mathrm{2}} \\ $$$$=\mathrm{4a}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{a}^{\mathrm{2}} \\ $$$$=\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\sqrt{\mathrm{3}}−\mathrm{3}\right)\mathrm{a}^{\mathrm{2}} \\ $$$$\approx\mathrm{82}.\mathrm{64}\:\mathrm{cm}^{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 27/Oct/17

$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{Can}\:\mathrm{it}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{even} \\ $$$$\mathrm{without}\:\mathrm{trigonomeric}\:\mathrm{ratios}. \\ $$
Commented by mrW1 last updated on 27/Oct/17

Commented by Joel577 last updated on 27/Oct/17

$${thank}\:{you}\:{very}\:{much} \\ $$
