Menu Close

Question-23253

Tinku Tara 0 Comments
Pin




Question Number 23253 by ajfour last updated on 28/Oct/17
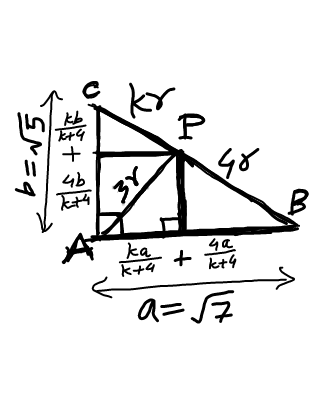
Commented by ajfour last updated on 28/Oct/17
Q.23251 (solution)
$${Q}.\mathrm{23251}\:\left({solution}\right) \\ $$
Commented by math solver last updated on 28/Oct/17
i didn′t get what you write in diagram
$$\:\mathrm{i}\:\mathrm{didn}'\mathrm{t}\:\mathrm{get}\:\mathrm{what}\:\mathrm{you}\:\mathrm{write}\:\mathrm{in}\:\mathrm{diagram} \\ $$
Commented by math solver last updated on 28/Oct/17
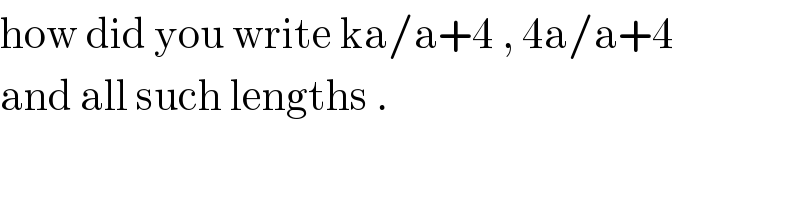
how did you write ka/a+4 , 4a/a+4 and all such lengths .
$$\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{write}\:\mathrm{ka}/\mathrm{a}+\mathrm{4}\:,\:\mathrm{4a}/\mathrm{a}+\mathrm{4} \\ $$$$\mathrm{and}\:\mathrm{all}\:\mathrm{such}\:\mathrm{lengths}\:. \\ $$
Commented by math solver last updated on 28/Oct/17
??
$$?? \\ $$
Commented by ajfour last updated on 28/Oct/17
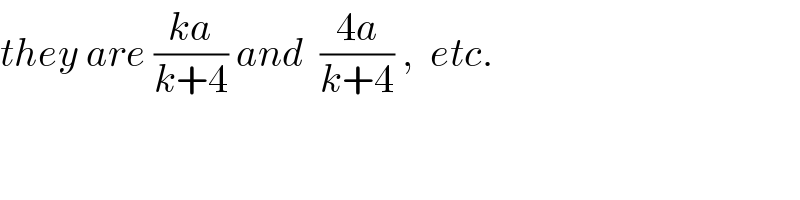
they are ((ka)/(k+4)) and ((4a)/(k+4)) , etc.
$${they}\:{are}\:\frac{{ka}}{{k}+\mathrm{4}}\:{and}\:\:\frac{\mathrm{4}{a}}{{k}+\mathrm{4}}\:,\:\:{etc}. \\ $$
Commented by math solver last updated on 28/Oct/17
yes i am asking these lengths only it is seem to written similar to that in case of incentre also . plz explain it?
$$\mathrm{yes}\:\mathrm{i}\:\mathrm{am}\:\mathrm{asking}\:\mathrm{these}\:\mathrm{lengths}\:\mathrm{only} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{written}\:\mathrm{similar}\:\mathrm{to}\: \\ $$$$\mathrm{that}\:\mathrm{in}\:\mathrm{case}\:\mathrm{of}\:\mathrm{incentre}\:\mathrm{also}\:.\:\mathrm{plz}\: \\ $$$$\mathrm{explain}\:\mathrm{it}? \\ $$
Commented by ajfour last updated on 28/Oct/17
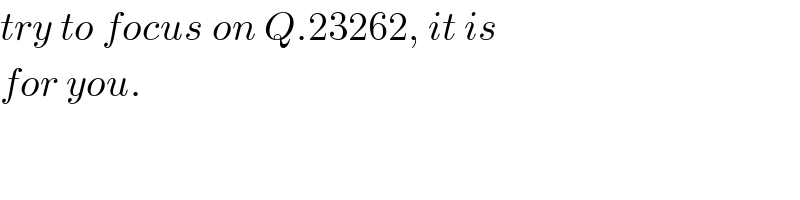
try to focus on Q.23262, it is for you.
$${try}\:{to}\:{focus}\:{on}\:{Q}.\mathrm{23262},\:{it}\:{is} \\ $$$${for}\:{you}. \\ $$
Commented by math solver last updated on 28/Oct/17
thank you sir !
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:! \\ $$
Answered by ajfour last updated on 28/Oct/17
BC^( 2) =AB^2 +AC^( 2) ⇒ (k+4)^2 r^2 = a^2 +b^2 ....(i) AP^( 2) =(((ka)/(k+4)))^2 +(((4b)/(k+4)))^2 =(3r)^2 ⇒ k^2 a^2 +16b^2 =9(k+4)^2 r^2 .....(ii) using (i) in (ii): k^2 a^2 +16b^2 =9(a^2 +b^2 ) ⇒ k=(√((9a^2 −7b^2 )/a^2 )) =(√(9−7((b/a))^2 )) as a=(√7) and b=(√5) we get k=2 ⇒ ((BP)/(PC)) =((4r)/(kr)) =(4/k)=(4/2)=(2/1) .
$$\:{BC}^{\:\mathrm{2}} ={AB}^{\mathrm{2}} +{AC}^{\:\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\left({k}+\mathrm{4}\right)^{\mathrm{2}} {r}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\:\:….\left({i}\right) \\ $$$${AP}^{\:\:\mathrm{2}} =\left(\frac{{ka}}{{k}+\mathrm{4}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}{b}}{{k}+\mathrm{4}}\right)^{\mathrm{2}} =\left(\mathrm{3}{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{k}^{\mathrm{2}} {a}^{\mathrm{2}} +\mathrm{16}{b}^{\mathrm{2}} =\mathrm{9}\left({k}+\mathrm{4}\right)^{\mathrm{2}} {r}^{\mathrm{2}} \:\:\:\:…..\left({ii}\right) \\ $$$${using}\:\left({i}\right)\:{in}\:\left({ii}\right): \\ $$$$\:\:\:\:\:\:\:{k}^{\mathrm{2}} {a}^{\mathrm{2}} +\mathrm{16}{b}^{\mathrm{2}} =\mathrm{9}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\Rightarrow\:\:\:{k}=\sqrt{\frac{\mathrm{9}{a}^{\mathrm{2}} −\mathrm{7}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{9}−\mathrm{7}\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} } \\ $$$${as}\:{a}=\sqrt{\mathrm{7}}\:{and}\:{b}=\sqrt{\mathrm{5}}\:{we}\:{get} \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{k}}=\mathrm{2} \\ $$$$\Rightarrow\:\:\:\:\frac{\boldsymbol{{BP}}}{\boldsymbol{{PC}}}\:=\frac{\mathrm{4}\boldsymbol{{r}}}{\boldsymbol{{kr}}}\:=\frac{\mathrm{4}}{\boldsymbol{{k}}}=\frac{\mathrm{4}}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{1}}\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *