Question Number 23262 by ajfour last updated on 28/Oct/17
Commented by ajfour last updated on 28/Oct/17
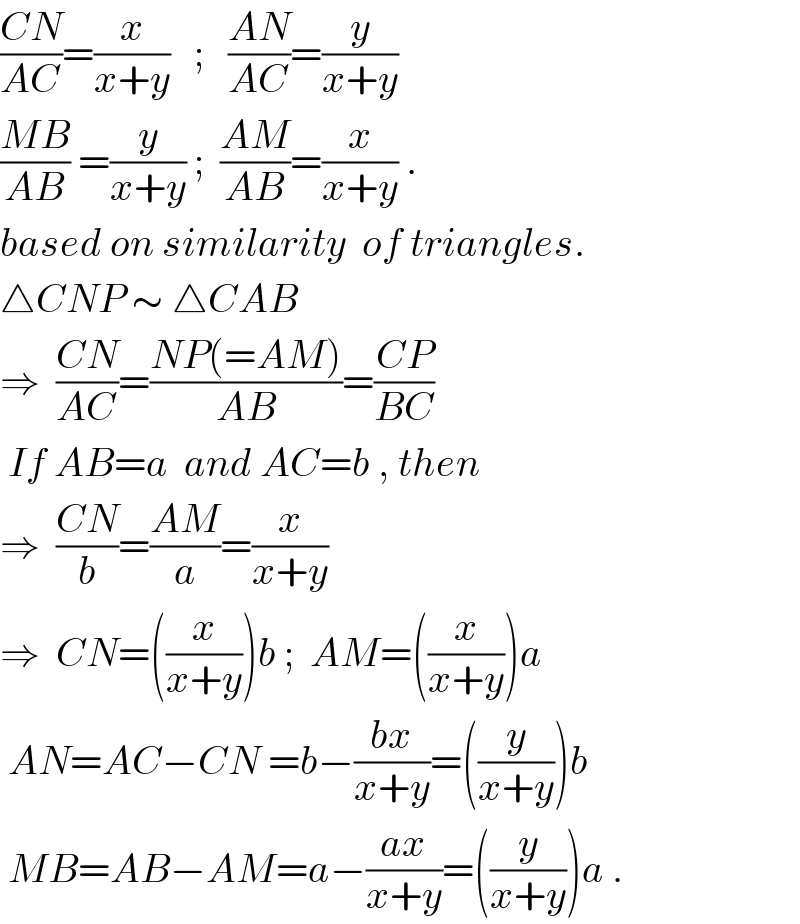
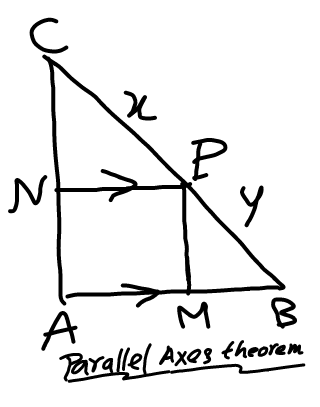
$$\frac{{CN}}{{AC}}=\frac{{x}}{{x}+{y}}\:\:\:;\:\:\:\frac{{AN}}{{AC}}=\frac{{y}}{{x}+{y}} \\ $$$$\frac{{MB}}{{AB}}\:=\frac{{y}}{{x}+{y}}\:;\:\:\frac{{AM}}{{AB}}=\frac{{x}}{{x}+{y}}\:. \\ $$$${based}\:{on}\:{similarity}\:\:{of}\:{triangles}. \\ $$$$\bigtriangleup{CNP}\:\sim\:\bigtriangleup{CAB} \\ $$$$\Rightarrow\:\:\frac{{CN}}{{AC}}=\frac{{NP}\left(={AM}\right)}{{AB}}=\frac{{CP}}{{BC}} \\ $$$$\:{If}\:{AB}={a}\:\:{and}\:{AC}={b}\:,\:{then} \\ $$$$\Rightarrow\:\:\frac{{CN}}{{b}}=\frac{{AM}}{{a}}=\frac{{x}}{{x}+{y}} \\ $$$$\Rightarrow\:\:{CN}=\left(\frac{{x}}{{x}+{y}}\right){b}\:;\:\:{AM}=\left(\frac{{x}}{{x}+{y}}\right){a} \\ $$$$\:{AN}={AC}−{CN}\:={b}−\frac{{bx}}{{x}+{y}}=\left(\frac{{y}}{{x}+{y}}\right){b} \\ $$$$\:{MB}={AB}−{AM}={a}−\frac{{ax}}{{x}+{y}}=\left(\frac{{y}}{{x}+{y}}\right){a}\:. \\ $$
Commented by ajfour last updated on 28/Oct/17
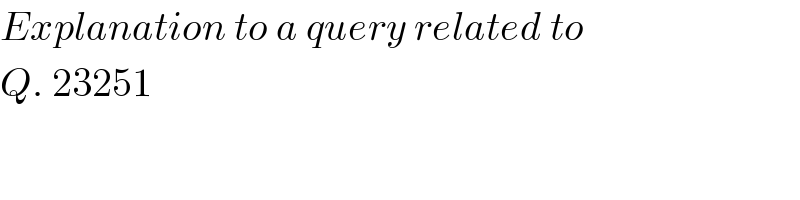
$${Explanation}\:{to}\:{a}\:{query}\:{related}\:{to} \\ $$$${Q}.\:\mathrm{23251} \\ $$
