Question Number 23334 by math solver last updated on 28/Oct/17
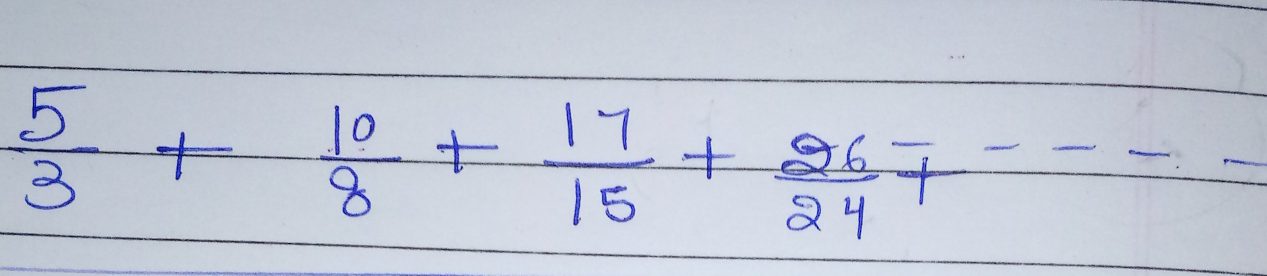
Commented by math solver last updated on 28/Oct/17
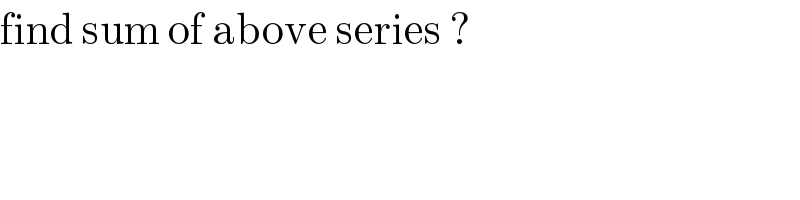
$$\mathrm{find}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{above}\:\mathrm{series}\:? \\ $$
Commented by ajfour last updated on 28/Oct/17
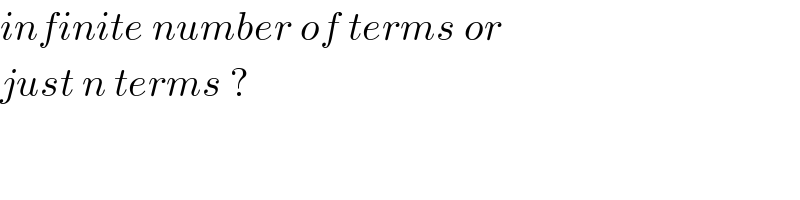
$${infinite}\:{number}\:{of}\:{terms}\:{or} \\ $$$${just}\:{n}\:{terms}\:? \\ $$
Commented by math solver last updated on 31/Oct/17

$$\mathrm{sir}\:,\:\mathrm{actually}\:\mathrm{i}\:\mathrm{made}\:\mathrm{this}\:\mathrm{problem} \\ $$$$\mathrm{myself}\:\mathrm{just}\:\mathrm{writing}\:\mathrm{N}_{\mathrm{r}} \:\mathrm{and}\:\mathrm{D}_{\mathrm{r}} \\ $$$$\mathrm{in}\:\mathrm{A}.\mathrm{P}\:.\:\left(\:\mathrm{take}\:\mathrm{infinite}\:\mathrm{terms}\right) \\ $$
Answered by ajfour last updated on 29/Oct/17
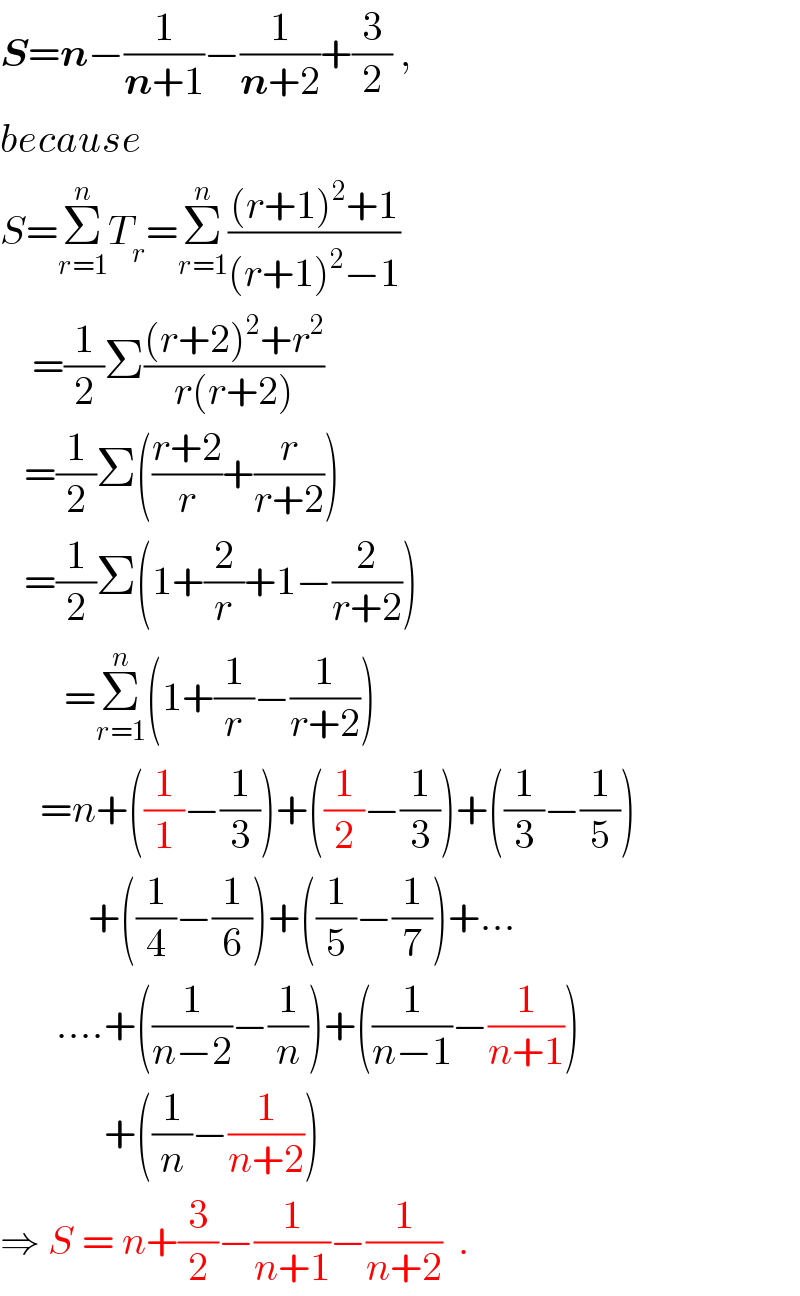
$$\boldsymbol{{S}}=\boldsymbol{{n}}−\frac{\mathrm{1}}{\boldsymbol{{n}}+\mathrm{1}}−\frac{\mathrm{1}}{\boldsymbol{{n}}+\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\:, \\ $$$${because} \\ $$$${S}=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{T}_{{r}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left({r}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{\left({r}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{\left({r}+\mathrm{2}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} }{{r}\left({r}+\mathrm{2}\right)} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left(\frac{{r}+\mathrm{2}}{{r}}+\frac{{r}}{{r}+\mathrm{2}}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left(\mathrm{1}+\frac{\mathrm{2}}{{r}}+\mathrm{1}−\frac{\mathrm{2}}{{r}+\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{1}+\frac{\mathrm{1}}{{r}}−\frac{\mathrm{1}}{{r}+\mathrm{2}}\right) \\ $$$$\:\:\:\:\:={n}+\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{6}}\right)+\left(\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}\right)+… \\ $$$$\:\:\:\:\:\:\:….+\left(\frac{\mathrm{1}}{{n}−\mathrm{2}}−\frac{\mathrm{1}}{{n}}\right)+\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)\: \\ $$$$\Rightarrow\:{S}\:=\:{n}+\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\:\:. \\ $$
