Question Number 23346 by ajfour last updated on 29/Oct/17
Commented by Physics lover last updated on 29/Oct/17

$${Nice}\:{trick}\:{sir}. \\ $$
Commented by ajfour last updated on 29/Oct/17

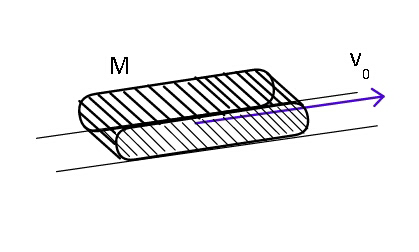
$${The}\:{centre}\:{of}\:{mass}\:{velocity}\:{of} \\ $$$${the}\:{conveyor}\:{belt}\:\:{vehicle}\:{of}\: \\ $$$${mass}\:{M}\:{rolling}\:{along}\:{a}\:{level}\: \\ $$$${road}\:{is}\:\boldsymbol{{v}}_{\mathrm{0}} .\boldsymbol{{F}}{ind}\:{its}\:{kinetic}\:{energy}. \\ $$
Commented by Physics lover last updated on 29/Oct/17
Commented by Physics lover last updated on 29/Oct/17
$${Sorry},{Mr}\:{Ajfour}\:,\:{I}\:{flagged}\:{this}\: \\ $$$${question}\:{by}\:{mistake}. \\ $$$${Did}\:{not}\:\:{intend}\:{to}\:{do}\:{so}\:{at}\:{all}. \\ $$
Commented by mrW1 last updated on 29/Oct/17
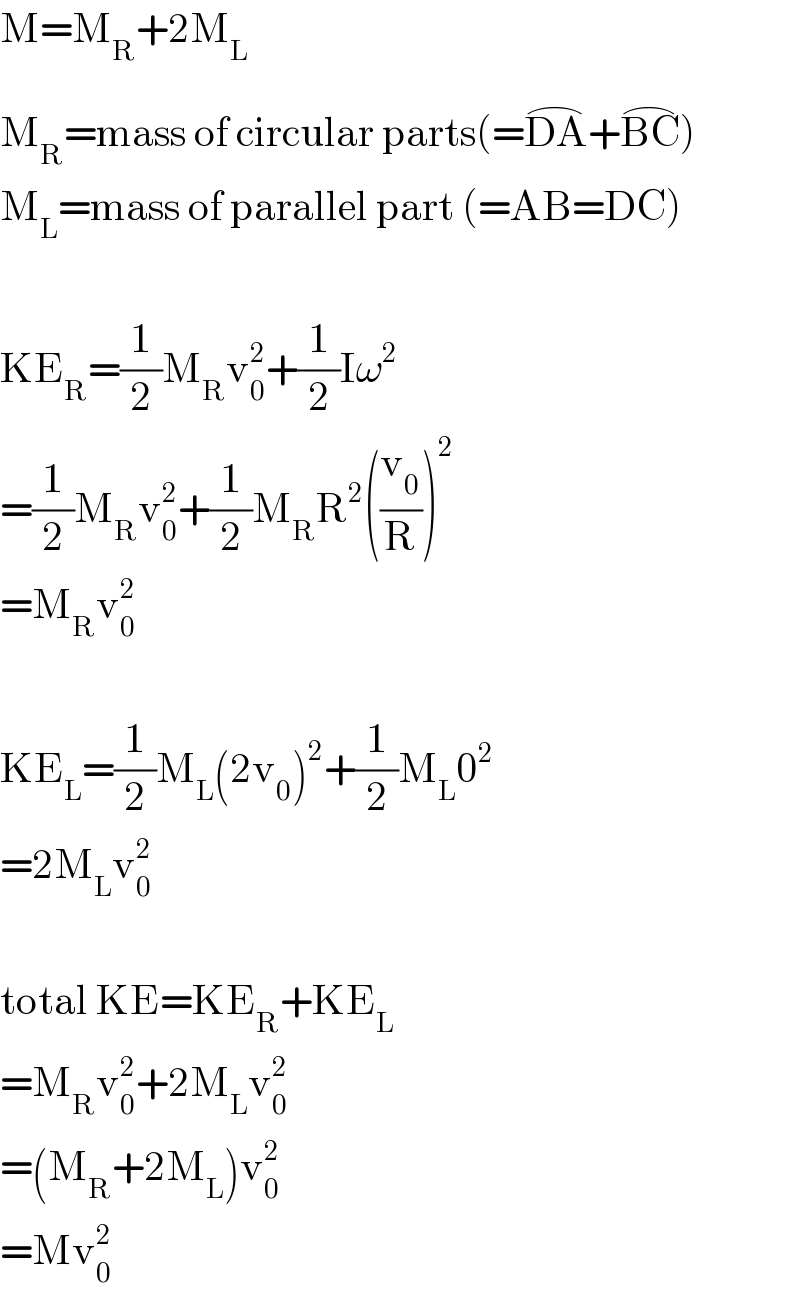
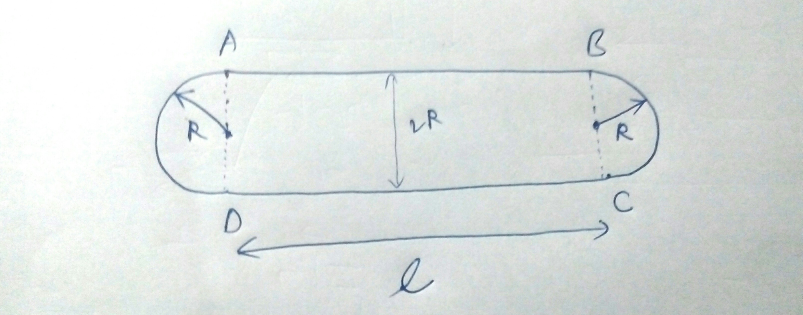
$$\mathrm{M}=\mathrm{M}_{\mathrm{R}} +\mathrm{2M}_{\mathrm{L}} \\ $$$$\mathrm{M}_{\mathrm{R}} =\mathrm{mass}\:\mathrm{of}\:\mathrm{circular}\:\mathrm{parts}\left(=\overset{\frown} {\mathrm{DA}}+\overset{\frown} {\mathrm{BC}}\right) \\ $$$$\mathrm{M}_{\mathrm{L}} =\mathrm{mass}\:\mathrm{of}\:\mathrm{parallel}\:\mathrm{part}\:\left(=\mathrm{AB}=\mathrm{DC}\right) \\ $$$$ \\ $$$$\mathrm{KE}_{\mathrm{R}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}_{\mathrm{R}} \mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}\omega^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}_{\mathrm{R}} \mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}_{\mathrm{R}} \mathrm{R}^{\mathrm{2}} \left(\frac{\mathrm{v}_{\mathrm{0}} }{\mathrm{R}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{M}_{\mathrm{R}} \mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{KE}_{\mathrm{L}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}_{\mathrm{L}} \left(\mathrm{2v}_{\mathrm{0}} \right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}_{\mathrm{L}} \mathrm{0}^{\mathrm{2}} \\ $$$$=\mathrm{2M}_{\mathrm{L}} \mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{total}\:\mathrm{KE}=\mathrm{KE}_{\mathrm{R}} +\mathrm{KE}_{\mathrm{L}} \\ $$$$=\mathrm{M}_{\mathrm{R}} \mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2M}_{\mathrm{L}} \mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\left(\mathrm{M}_{\mathrm{R}} +\mathrm{2M}_{\mathrm{L}} \right)\mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\mathrm{Mv}_{\mathrm{0}} ^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 29/Oct/17
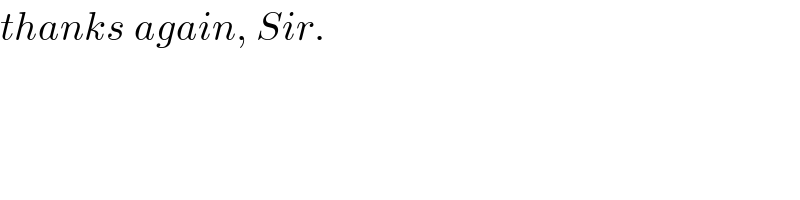
$${thanks}\:{again},\:{Sir}. \\ $$
Commented by ajfour last updated on 29/Oct/17
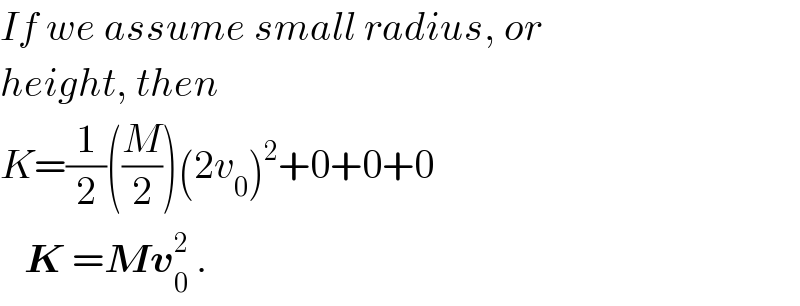
$${If}\:{we}\:{assume}\:{small}\:{radius},\:{or} \\ $$$${height},\:{then} \\ $$$${K}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{M}}{\mathrm{2}}\right)\left(\mathrm{2}{v}_{\mathrm{0}} \right)^{\mathrm{2}} +\mathrm{0}+\mathrm{0}+\mathrm{0} \\ $$$$\:\:\:\boldsymbol{{K}}\:=\boldsymbol{{Mv}}_{\mathrm{0}} ^{\mathrm{2}} \:. \\ $$
Answered by Physics lover last updated on 29/Oct/17
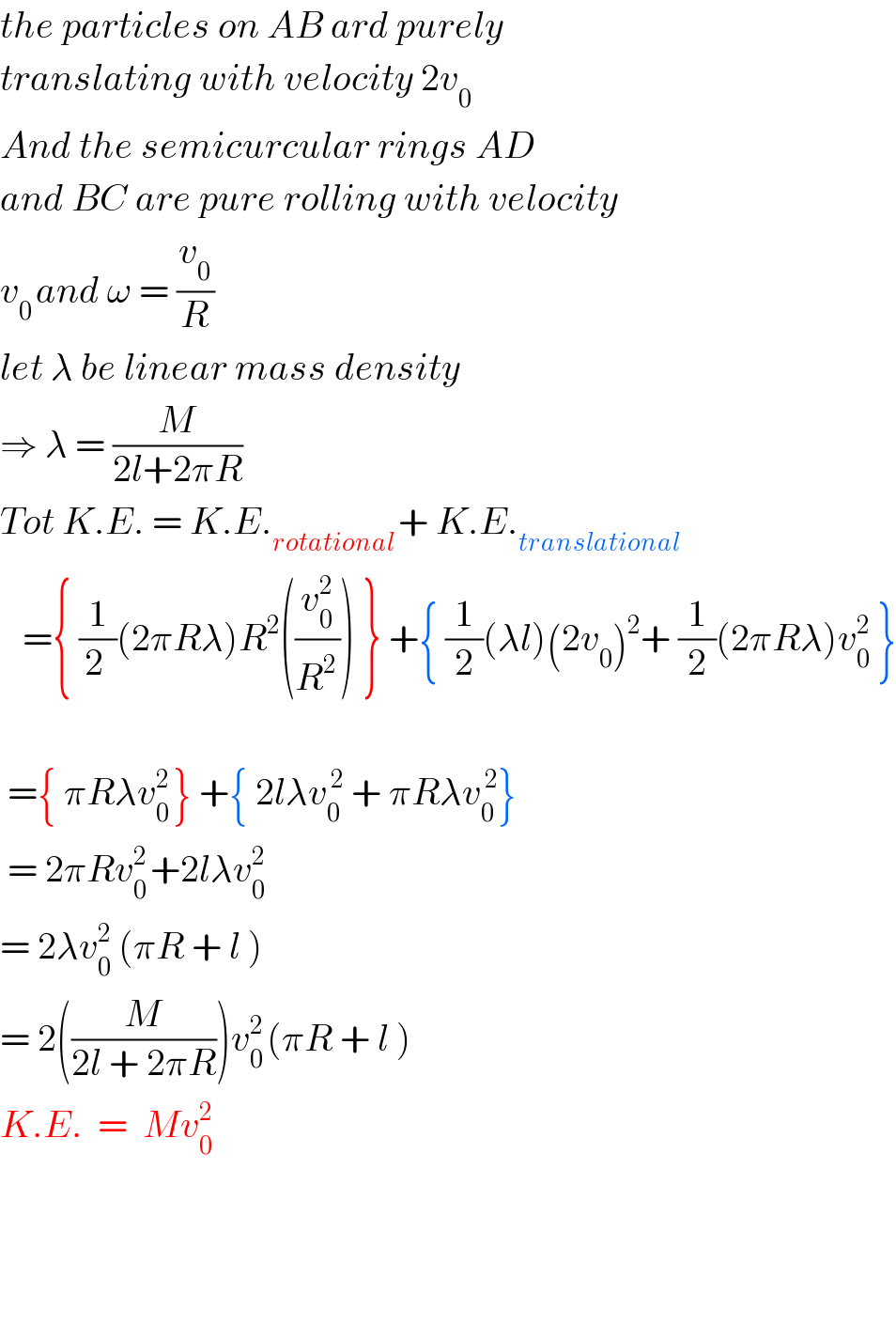
$${the}\:{particles}\:{on}\:{AB}\:{ard}\:{purely}\: \\ $$$${translating}\:{with}\:{velocity}\:\mathrm{2}{v}_{\mathrm{0}} \\ $$$${And}\:{the}\:{semicurcular}\:{rings}\:{AD} \\ $$$${and}\:{BC}\:{are}\:{pure}\:{rolling}\:{with}\:{velocity} \\ $$$${v}_{\mathrm{0}\:} {and}\:\omega\:=\:\frac{{v}_{\mathrm{0}} }{{R}} \\ $$$${let}\:\lambda\:{be}\:{linear}\:{mass}\:{density} \\ $$$$\Rightarrow\:\lambda\:=\:\frac{{M}}{\mathrm{2}{l}+\mathrm{2}\pi{R}} \\ $$$${Tot}\:{K}.{E}.\:=\:{K}.{E}._{{rotational}\:} +\:{K}.{E}._{{translational}} \\ $$$$\:\:\:=\left\{\:\frac{\mathrm{1}}{\mathrm{2}\:}\left(\mathrm{2}\pi{R}\lambda\right){R}^{\mathrm{2}} \left(\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{{R}^{\mathrm{2}\:} }\right)\:\right\}\:+\left\{\:\frac{\mathrm{1}}{\mathrm{2}}\left(\lambda{l}\right)\left(\mathrm{2}{v}_{\mathrm{0}} \right)^{\mathrm{2}} +\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\pi{R}\lambda\right){v}_{\mathrm{0}} ^{\mathrm{2}} \:\right\} \\ $$$$\:\: \\ $$$$\:=\left\{\:\pi{R}\lambda{v}_{\mathrm{0}} ^{\mathrm{2}\:} \right\}\:+\left\{\:\mathrm{2}{l}\lambda{v}_{\mathrm{0}} ^{\:\mathrm{2}} \:+\:\pi{R}\lambda{v}_{\mathrm{0}\:} ^{\:\mathrm{2}} \right\} \\ $$$$\:=\:\mathrm{2}\pi{Rv}_{\mathrm{0}} ^{\mathrm{2}\:} +\mathrm{2}{l}\lambda{v}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\:\mathrm{2}\lambda{v}_{\mathrm{0}} ^{\mathrm{2}} \:\left(\pi{R}\:+\:{l}\:\right) \\ $$$$=\:\mathrm{2}\left(\frac{{M}}{\mathrm{2}{l}\:+\:\mathrm{2}\pi{R}}\right){v}_{\mathrm{0}} ^{\mathrm{2}\:} \left(\pi{R}\:+\:{l}\:\right) \\ $$$${K}.{E}.\:\:=\:\:{Mv}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 29/Oct/17
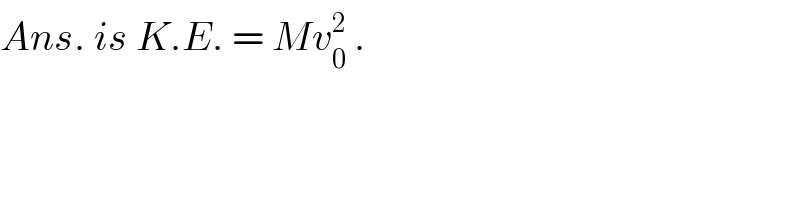
$${Ans}.\:{is}\:{K}.{E}.\:=\:{Mv}_{\mathrm{0}} ^{\mathrm{2}} \:. \\ $$
Commented by ajfour last updated on 29/Oct/17
$${Thank}\:{you}\:{Physics}\:{lover}. \\ $$
Commented by Physics lover last updated on 29/Oct/17
$${You}\:{are}\:{welcome}\:{sir}.\:{But}\:{i}\:{guess} \\ $$$${i}\:{did}\:{it}\:{in}\:{the}\:{most}\:{lengthy}\:{way}.{lol} \\ $$
Commented by ajfour last updated on 29/Oct/17

$${Your}\:{proof}\:{is}\:{quite}\:{general}\:{one} \\ $$$$\left({answer}\:{to}\:{a}\:{subjective}\:{question}\right). \\ $$
Commented by Physics lover last updated on 29/Oct/17
$$\left.{Oh}\:{thank}\:{you}\:{sir}.\:\::\right) \\ $$
