Menu Close

Question-23419

Tinku Tara 0 Comments
Pin




Question Number 23419 by mondodotto@gmail.com last updated on 30/Oct/17
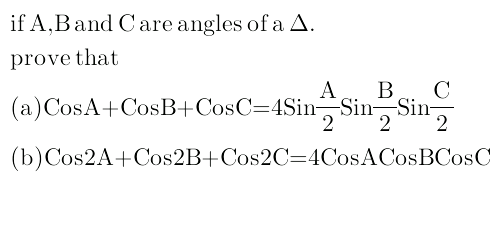
Answered by $@ty@m last updated on 31/Oct/17
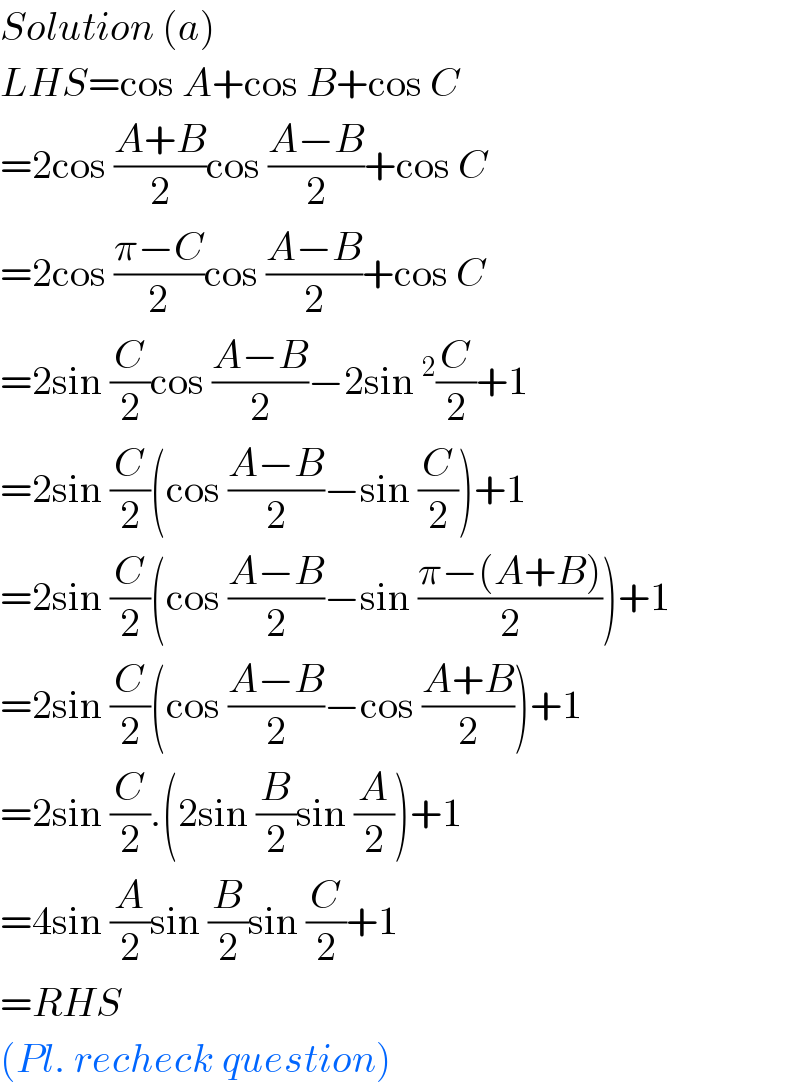
Solution (a) LHS=cos A+cos B+cos C =2cos ((A+B)/2)cos ((A−B)/2)+cos C =2cos ((π−C)/2)cos ((A−B)/2)+cos C =2sin (C/2)cos ((A−B)/2)−2sin^2 (C/2)+1 =2sin (C/2)(cos ((A−B)/2)−sin (C/2))+1 =2sin (C/2)(cos ((A−B)/2)−sin ((π−(A+B))/2))+1 =2sin (C/2)(cos ((A−B)/2)−cos ((A+B)/2))+1 =2sin (C/2).(2sin (B/2)sin (A/2))+1 =4sin (A/2)sin (B/2)sin (C/2)+1 =RHS (Pl. recheck question)
$${Solution}\:\left({a}\right) \\ $$$${LHS}=\mathrm{cos}\:{A}+\mathrm{cos}\:{B}+\mathrm{cos}\:{C} \\ $$$$=\mathrm{2cos}\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}+\mathrm{cos}\:{C} \\ $$$$=\mathrm{2cos}\:\frac{\pi−{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}+\mathrm{cos}\:{C} \\ $$$$=\mathrm{2sin}\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}−\mathrm{2sin}\:^{\mathrm{2}} \frac{{C}}{\mathrm{2}}+\mathrm{1} \\ $$$$=\mathrm{2sin}\:\frac{{C}}{\mathrm{2}}\left(\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}−\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\right)+\mathrm{1} \\ $$$$=\mathrm{2sin}\:\frac{{C}}{\mathrm{2}}\left(\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}−\mathrm{sin}\:\frac{\pi−\left({A}+{B}\right)}{\mathrm{2}}\right)+\mathrm{1} \\ $$$$=\mathrm{2sin}\:\frac{{C}}{\mathrm{2}}\left(\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}−\mathrm{cos}\:\frac{{A}+{B}}{\mathrm{2}}\right)+\mathrm{1} \\ $$$$=\mathrm{2sin}\:\frac{{C}}{\mathrm{2}}.\left(\mathrm{2sin}\:\frac{{B}}{\mathrm{2}}\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\right)+\mathrm{1} \\ $$$$=\mathrm{4sin}\:\frac{{A}}{\mathrm{2}}\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\mathrm{sin}\:\frac{{C}}{\mathrm{2}}+\mathrm{1} \\ $$$$={RHS} \\ $$$$\left({Pl}.\:{recheck}\:{question}\right) \\ $$
Answered by $@ty@m last updated on 31/Oct/17
Solution (b) LHS=cos 2A+cos 2B+cos 2C =2cos (A+B)cos (A−B)+cos 2C =2cos (π−C)cos (A−B)+cos 2C =−2cos Ccos (A−B)+2cos^2 C−1 =−2cos C{cos (A−B)−cos C}−1 =−2cos C(2cosAcos B) −1 =−4cos CcosAcos B −1
$${Solution}\:\left({b}\right) \\ $$$${LHS}=\mathrm{cos}\:\mathrm{2}{A}+\mathrm{cos}\:\mathrm{2}{B}+\mathrm{cos}\:\mathrm{2}{C} \\ $$$$=\mathrm{2cos}\:\left({A}+{B}\right)\mathrm{cos}\:\left({A}−{B}\right)+\mathrm{cos}\:\mathrm{2}{C} \\ $$$$=\mathrm{2cos}\:\left(\pi−{C}\right)\mathrm{cos}\:\left({A}−{B}\right)+\mathrm{cos}\:\mathrm{2}{C} \\ $$$$=−\mathrm{2cos}\:{C}\mathrm{cos}\:\left({A}−{B}\right)+\mathrm{2cos}\:^{\mathrm{2}} {C}−\mathrm{1} \\ $$$$=−\mathrm{2cos}\:{C}\left\{\mathrm{cos}\:\left({A}−{B}\right)−\mathrm{cos}\:{C}\right\}−\mathrm{1} \\ $$$$=−\mathrm{2cos}\:{C}\left(\mathrm{2cos}{A}\mathrm{cos}\:{B}\right)\:−\mathrm{1} \\ $$$$=−\mathrm{4cos}\:{C}\mathrm{cos}{A}\mathrm{cos}\:{B}\:−\mathrm{1} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *