Question-23472

Question Number 23472 by ajfour last updated on 31/Oct/17

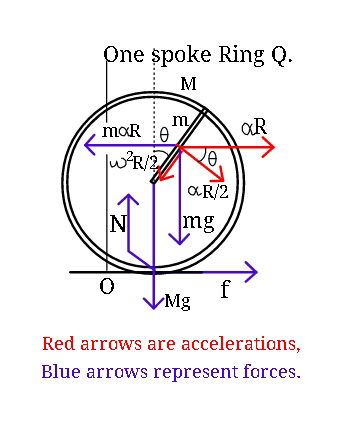
Commented by ajfour last updated on 31/Oct/17

Q . 23390 (c o n t i n u e d . .)

Answered by ajfour last updated on 31/Oct/17

A p p l y i n g Σ F_{x} = Σ {m a}_{x} f r o m t h e

g r o u n d f r a m e :

f = (M + m) (α R) + \frac{m (α R) \cos θ}{2}

- m ω^{2} (\frac{R}{2}) \sin θ \dots (i)

A p p l y i n g Σ τ = I_{n e t} α f r o m t h e

f r a m e o f c e n t r e o f r i n g :

\frac{m g R \sin θ}{2} - f R - (m α R) (\frac{R}{2} \cos θ)

= ({M R}^{2} + \frac{{m R}^{2}}{3}) α \dots (i i)

e l i m i n a t i n g f f r o m (i) a n d (i i) :

\frac{m g \sin θ}{2} - (M + m) (α R)

- \frac{m (α R) \cos θ}{2} + \frac{m ω^{2} R \sin θ}{2}

- \frac{m (α R) \cos θ}{2} = (M + \frac{m}{3}) (α R)

\Rightarrow (α R) [M + \frac{m}{3} + M + m + m \cos θ]

= \frac{m \sin θ}{2} (ω^{2} R + g)

\Rightarrow α = \frac{m (ω^{2} + g / R) \sin θ}{2 [2 M + \frac{4 m}{3} + m \cos θ]}

\Rightarrow \frac{ω d ω}{d θ} = \frac{m (ω^{2} + \frac{g}{R}) \sin θ}{2 [2 M + \frac{4 m}{3} + m \cos θ]}

\int_{0}^{ω} \frac{2 ω d ω}{ω^{2} + \frac{g}{R}} = \int_{0}^{θ} \frac{m \sin θ}{2 M + \frac{4 m}{3} + m \cos θ}

\ln (\frac{ω^{2} + \frac{g}{R}}{\frac{g}{R}}) = \ln (\frac{2 M + \frac{4 m}{3} + m}{2 M + \frac{4 m}{3} + m \cos θ})

\frac{ω^{2} R}{g} + 1 = 1 - \frac{m (1 - \cos θ)}{2 M + \frac{4 m}{3} + m \cos θ}

ω^{2} = \frac{g}{R} (\frac{1 - \cos θ}{\frac{2 M}{m} + \frac{4}{3} + \cos θ})

A n d α = \frac{1}{2} \frac{d (ω^{2})}{d θ} .

T o o b t a i n t h e t i m e f o r t h e r e t u r n,

\Rightarrow ω = \frac{d θ}{d t} = \sqrt{\frac{g}{R}} {[\frac{1 - \cos θ}{b^{2} + \cos θ}]}^{1 / 2}

\Rightarrow T = 4 \sqrt{\frac{R}{g}} \int_{0}^{π} {[\frac{b^{2} + \cos θ}{1 - \cos θ}]}^{1 / 2} d θ

w h e r e b^{2} = \frac{2 M}{m} + \frac{4}{3} .

\dots . m i g h t c o n t i n u e \dots

Commented by mrW1 last updated on 31/Oct/17

how is it to explain, that the time

from θ = 0 is not convergent ?

Facebook Tweet Pin