Question Number 23492 by ajfour last updated on 31/Oct/17
Commented by ajfour last updated on 31/Oct/17

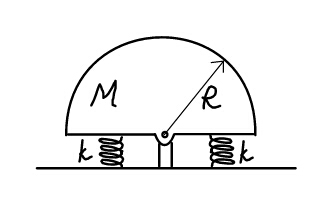
$$\:\:\:\:\:\:\:{Find}\:{the}\:{period}\:{of}\:{small}\: \\ $$$$\:\:\:\:\:{oscillations}\:{of}\:{the}\:{disc},\:{if} \\ $$$$\:\:\:\:\:\:{springs}\:{are}\:{attached}\:{at}\:{a}\: \\ $$$$\:\:\:\:\:\:\:\:{distance}\:{of}\:\boldsymbol{{a}}\:{from}\:{the} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{frictionless}\:{hinge}. \\ $$
Commented by mrW1 last updated on 31/Oct/17
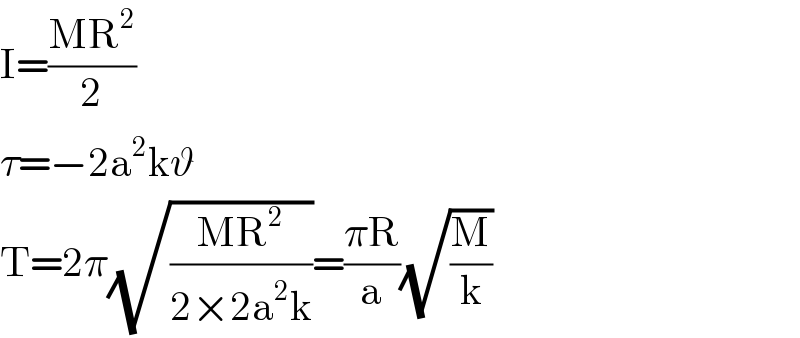
$$\mathrm{I}=\frac{\mathrm{MR}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\tau=−\mathrm{2a}^{\mathrm{2}} \mathrm{k}\vartheta \\ $$$$\mathrm{T}=\mathrm{2}\pi\sqrt{\frac{\mathrm{MR}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2a}^{\mathrm{2}} \mathrm{k}}}=\frac{\pi\mathrm{R}}{\mathrm{a}}\sqrt{\frac{\mathrm{M}}{\mathrm{k}}} \\ $$
Commented by ajfour last updated on 31/Oct/17
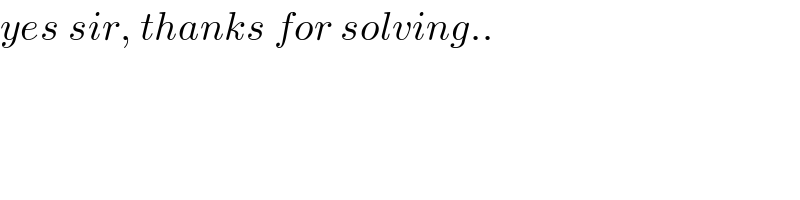
$${yes}\:{sir},\:{thanks}\:{for}\:{solving}.. \\ $$
Commented by ajfour last updated on 31/Oct/17

$${Mg}\:{even}\:{contributes}\:{a}\:{positive} \\ $$$${torque}..{shouldn}'{t}\:{that}\:{be}\:{even}\: \\ $$$${taken}\:{into}\:{account}\:? \\ $$
Commented by mrW1 last updated on 31/Oct/17
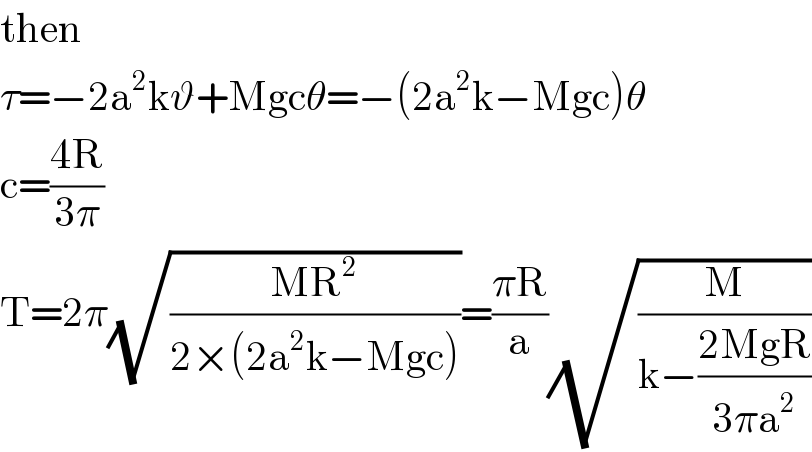
$$\mathrm{then} \\ $$$$\tau=−\mathrm{2a}^{\mathrm{2}} \mathrm{k}\vartheta+\mathrm{Mgc}\theta=−\left(\mathrm{2a}^{\mathrm{2}} \mathrm{k}−\mathrm{Mgc}\right)\theta \\ $$$$\mathrm{c}=\frac{\mathrm{4R}}{\mathrm{3}\pi} \\ $$$$\mathrm{T}=\mathrm{2}\pi\sqrt{\frac{\mathrm{MR}^{\mathrm{2}} }{\mathrm{2}×\left(\mathrm{2a}^{\mathrm{2}} \mathrm{k}−\mathrm{Mgc}\right)}}=\frac{\pi\mathrm{R}}{\mathrm{a}}\sqrt{\frac{\mathrm{M}}{\mathrm{k}−\frac{\mathrm{2MgR}}{\mathrm{3}\pi\mathrm{a}^{\mathrm{2}} }}} \\ $$
