Question Number 23531 by ajfour last updated on 01/Nov/17

Commented by ajfour last updated on 01/Nov/17

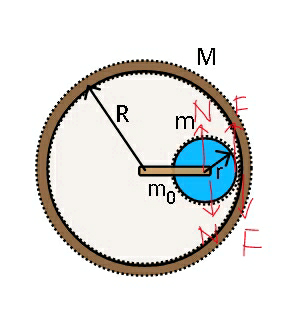
$${If}\:{the}\:{system}\:{consisting}\:{of}\:{a} \\ $$$${ring}\:{of}\:{radius}\:\boldsymbol{{R}},\:{mass}\:\boldsymbol{{M}},\:{mounted} \\ $$$${on}\:{a}\:{horizontal}\:{axis}\:{with}\:{a}\:{disc} \\ $$$${of}\:{radius}\:\boldsymbol{{r}},\:{mass}\:\boldsymbol{{m}}\:{connected}\: \\ $$$${as}\:{shown},\:{through}\:{a}\:{rod}\:{of}\:{mass}\:{m}_{\mathrm{0}} \: \\ $$$${be}\:{released}\:{as}\:{shown};\:{find}\:{the} \\ $$$${initial}\:\:{angular}\:{accelerations} \\ $$$${of}\:{rod},\:{disc}\left({about}\:{its}\:{centre}\right),\: \\ $$$${and}\:{ring}. \\ $$$${For}\:{a}\:{much}\:{simpler}\:{case} \\ $$$${please}\:{assume}\:\boldsymbol{{R}}=\mathrm{3}\boldsymbol{{r}}\:{and} \\ $$$$\:\:\:\:\boldsymbol{{M}}=\boldsymbol{{m}}=\boldsymbol{{m}}_{\mathrm{0}} \:. \\ $$
Commented by ajfour last updated on 01/Nov/17

$${does}\:{this}\:{help}\:{you}\:{figure}\:{the} \\ $$$${situation}\:{sir},\:{everwhere}\:{turning} \\ $$$${is}\:{allowed},\:{frictionless}\:{bearings} \\ $$$${are}\:{present}.\:{The}\:{ring}\:{is}\:{mounted} \\ $$$${on}\:{a}\:{horizontal}\:{axis}\:\Rightarrow\:{it}\:{is}\:{free} \\ $$$${to}\:{turn}\:{about}\:{it}\:{in}\:{a}\:{vertical}\:{plane}. \\ $$
Commented by mrW1 last updated on 01/Nov/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{this}\:\mathrm{info}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{try}. \\ $$
Answered by mrW1 last updated on 01/Nov/17
![let O=center point of ring let C=center point of disc θ=rotation of bar (rod) about O ϕ=rotation of disc about C φ=rotation of ring about O φ=θ(1−(r/R))+(r/R)ϕ α_B =angular acceleration of bar α_D =angular acceleration of disc α_R =angular acceleration of ring ⇒α_R =(1−(r/R))α_B +(r/R)α_D I_R =MR^2 for ring I_D =((mr^2 )/2) for disc I_B =((m_0 (R−r)^2 )/3) for bar (rod) let F=vertical force between disc and ring let N=vertical force between bar and disc I_R α_R =F×R ...(i) I_D α_D =−F×r ...(ii) ma_D =mα_B (R−r)=mg+N−F ...(iii) I_B α_B =m_0 g×((R−r)/2)−N(R−r) ...(iv) from (ii) ⇒ F=−(I_D /r)α_D from (iii) ⇒ N=m(R−r)α_B −mg+F ⇒ N=m(R−r)α_B −mg−(I_D /r)α_D from (i) ⇒ I_R α_R =−(R/r)×I_D α_D ⇒ I_R [(1−(r/R))α_B +(r/R)α_D ]=−(R/r)×I_D α_D ⇒ (1−(r/R))I_R α_B =−((r/R)×I_R +(R/r)×I_D )α_D ⇒ α_B =−(r/(R−r))×[1+(R^2 /r^2 )×(I_D /I_R )]α_D ...(v) from (iv) ⇒ I_B α_B =(R−r)[(((2m+m_0 )g)/2)−m(R−r)α_B +(I_D /r) α_D ] ⇒ I_B α_B =(((2m+m_0 )(R−r)g)/2)−m(R−r)^2 α_B +(R−r)(I_D /r) α_D ⇒[ I_B +m(R−r)^2 ]α_B =(m+(m_0 /2))(R−r)g+((R/r)−1)I_D α_D ⇒{(r/(R−r))×[ I_B +m(R−r)^2 ]×[1+(R^2 /r^2 )×(I_D /I_R )]+((R/r)−1)I_D }α_D =−(m+(m_0 /2))(R−r)g ⇒ α_D =−(((m+(m_0 /2))(R−r)g)/([ (r/(R−r))×I_B +mr(R−r)](1+(R^2 /r^2 )×(I_D /I_R ))+((R/r)−1)I_D )) ⇒ α_B =−(r/(R−r))(1+(R^2 /r^2 )×(I_D /I_R ))α_D ⇒α_R =(1−(r/R))α_B +(r/R)α_D for R=3r and M=m_0 =m, we get I_R =MR^2 =9mr^2 I_D =((mr^2 )/2) I_B =((m_0 (R−r)^2 )/3)=((4mr^2 )/3) ⇒ α_D =−(3/5)×(g/r) (↶) for disc ⇒ α_B =(9/(20))×(g/r) (↷) for rod ⇒α_R =(1/(10))×(g/r) (↷) for ring](https://www.tinkutara.com/question/Q23552.png)
$$\mathrm{let}\:\mathrm{O}=\mathrm{center}\:\mathrm{point}\:\mathrm{of}\:\mathrm{ring} \\ $$$$\mathrm{let}\:\mathrm{C}=\mathrm{center}\:\mathrm{point}\:\mathrm{of}\:\mathrm{disc} \\ $$$$\theta=\mathrm{rotation}\:\mathrm{of}\:\mathrm{bar}\:\left(\mathrm{rod}\right)\:\mathrm{about}\:\mathrm{O} \\ $$$$\varphi=\mathrm{rotation}\:\mathrm{of}\:\mathrm{disc}\:\mathrm{about}\:\mathrm{C} \\ $$$$\phi=\mathrm{rotation}\:\mathrm{of}\:\mathrm{ring}\:\mathrm{about}\:\mathrm{O} \\ $$$$ \\ $$$$\phi=\theta\left(\mathrm{1}−\frac{\mathrm{r}}{\mathrm{R}}\right)+\frac{\mathrm{r}}{\mathrm{R}}\varphi \\ $$$$\alpha_{\mathrm{B}} =\mathrm{angular}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{bar} \\ $$$$\alpha_{\mathrm{D}} =\mathrm{angular}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{disc} \\ $$$$\alpha_{\mathrm{R}} =\mathrm{angular}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{ring} \\ $$$$\Rightarrow\alpha_{\mathrm{R}} =\left(\mathrm{1}−\frac{\mathrm{r}}{\mathrm{R}}\right)\alpha_{\mathrm{B}} +\frac{\mathrm{r}}{\mathrm{R}}\alpha_{\mathrm{D}} \\ $$$$ \\ $$$$\mathrm{I}_{\mathrm{R}} =\mathrm{MR}^{\mathrm{2}} \:\mathrm{for}\:\mathrm{ring} \\ $$$$\mathrm{I}_{\mathrm{D}} =\frac{\mathrm{mr}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{for}\:\mathrm{disc} \\ $$$$\mathrm{I}_{\mathrm{B}} =\frac{\mathrm{m}_{\mathrm{0}} \left(\mathrm{R}−\mathrm{r}\right)^{\mathrm{2}} }{\mathrm{3}}\:\mathrm{for}\:\mathrm{bar}\:\left(\mathrm{rod}\right) \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{F}=\mathrm{vertical}\:\mathrm{force}\:\mathrm{between}\:\mathrm{disc}\:\mathrm{and}\:\mathrm{ring} \\ $$$$\mathrm{let}\:\mathrm{N}=\mathrm{vertical}\:\mathrm{force}\:\mathrm{between}\:\mathrm{bar}\:\mathrm{and}\:\mathrm{disc} \\ $$$$ \\ $$$$\mathrm{I}_{\mathrm{R}} \alpha_{\mathrm{R}} =\mathrm{F}×\mathrm{R}\:\:\:…\left(\mathrm{i}\right) \\ $$$$\mathrm{I}_{\mathrm{D}} \alpha_{\mathrm{D}} =−\mathrm{F}×\mathrm{r}\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\mathrm{ma}_{\mathrm{D}} =\mathrm{m}\alpha_{\mathrm{B}} \left(\mathrm{R}−\mathrm{r}\right)=\mathrm{mg}+\mathrm{N}−\mathrm{F}\:\:\:…\left(\mathrm{iii}\right) \\ $$$$\mathrm{I}_{\mathrm{B}} \alpha_{\mathrm{B}} =\mathrm{m}_{\mathrm{0}} \mathrm{g}×\frac{\mathrm{R}−\mathrm{r}}{\mathrm{2}}−\mathrm{N}\left(\mathrm{R}−\mathrm{r}\right)\:\:\:…\left(\mathrm{iv}\right) \\ $$$$ \\ $$$$\mathrm{from}\:\left(\mathrm{ii}\right) \\ $$$$\Rightarrow\:\mathrm{F}=−\frac{\mathrm{I}_{\mathrm{D}} }{\mathrm{r}}\alpha_{\mathrm{D}} \\ $$$$\mathrm{from}\:\left(\mathrm{iii}\right) \\ $$$$\Rightarrow\:\mathrm{N}=\mathrm{m}\left(\mathrm{R}−\mathrm{r}\right)\alpha_{\mathrm{B}} −\mathrm{mg}+\mathrm{F} \\ $$$$\Rightarrow\:\mathrm{N}=\mathrm{m}\left(\mathrm{R}−\mathrm{r}\right)\alpha_{\mathrm{B}} −\mathrm{mg}−\frac{\mathrm{I}_{\mathrm{D}} }{\mathrm{r}}\alpha_{\mathrm{D}} \\ $$$$\mathrm{from}\:\left(\mathrm{i}\right) \\ $$$$\Rightarrow\:\mathrm{I}_{\mathrm{R}} \alpha_{\mathrm{R}} =−\frac{\mathrm{R}}{\mathrm{r}}×\mathrm{I}_{\mathrm{D}} \alpha_{\mathrm{D}} \\ $$$$\Rightarrow\:\mathrm{I}_{\mathrm{R}} \left[\left(\mathrm{1}−\frac{\mathrm{r}}{\mathrm{R}}\right)\alpha_{\mathrm{B}} +\frac{\mathrm{r}}{\mathrm{R}}\alpha_{\mathrm{D}} \right]=−\frac{\mathrm{R}}{\mathrm{r}}×\mathrm{I}_{\mathrm{D}} \alpha_{\mathrm{D}} \\ $$$$\Rightarrow\:\left(\mathrm{1}−\frac{\mathrm{r}}{\mathrm{R}}\right)\mathrm{I}_{\mathrm{R}} \alpha_{\mathrm{B}} =−\left(\frac{\mathrm{r}}{\mathrm{R}}×\mathrm{I}_{\mathrm{R}} +\frac{\mathrm{R}}{\mathrm{r}}×\mathrm{I}_{\mathrm{D}} \right)\alpha_{\mathrm{D}} \\ $$$$\Rightarrow\:\alpha_{\mathrm{B}} =−\frac{\mathrm{r}}{\mathrm{R}−\mathrm{r}}×\left[\mathrm{1}+\frac{\mathrm{R}^{\mathrm{2}} }{\mathrm{r}^{\mathrm{2}} }×\frac{\mathrm{I}_{\mathrm{D}} }{\mathrm{I}_{\mathrm{R}} }\right]\alpha_{\mathrm{D}} \:\:\:…\left(\mathrm{v}\right) \\ $$$$ \\ $$$$\mathrm{from}\:\left(\mathrm{iv}\right) \\ $$$$\Rightarrow\:\mathrm{I}_{\mathrm{B}} \alpha_{\mathrm{B}} =\left(\mathrm{R}−\mathrm{r}\right)\left[\frac{\left(\mathrm{2m}+\mathrm{m}_{\mathrm{0}} \right)\mathrm{g}}{\mathrm{2}}−\mathrm{m}\left(\mathrm{R}−\mathrm{r}\right)\alpha_{\mathrm{B}} +\frac{\mathrm{I}_{\mathrm{D}} }{\mathrm{r}}\:\alpha_{\mathrm{D}} \right] \\ $$$$\Rightarrow\:\mathrm{I}_{\mathrm{B}} \alpha_{\mathrm{B}} =\frac{\left(\mathrm{2m}+\mathrm{m}_{\mathrm{0}} \right)\left(\mathrm{R}−\mathrm{r}\right)\mathrm{g}}{\mathrm{2}}−\mathrm{m}\left(\mathrm{R}−\mathrm{r}\right)^{\mathrm{2}} \alpha_{\mathrm{B}} +\left(\mathrm{R}−\mathrm{r}\right)\frac{\mathrm{I}_{\mathrm{D}} }{\mathrm{r}}\:\alpha_{\mathrm{D}} \\ $$$$\Rightarrow\left[\:\mathrm{I}_{\mathrm{B}} +\mathrm{m}\left(\mathrm{R}−\mathrm{r}\right)^{\mathrm{2}} \right]\alpha_{\mathrm{B}} =\left(\mathrm{m}+\frac{\mathrm{m}_{\mathrm{0}} }{\mathrm{2}}\right)\left(\mathrm{R}−\mathrm{r}\right)\mathrm{g}+\left(\frac{\mathrm{R}}{\mathrm{r}}−\mathrm{1}\right)\mathrm{I}_{\mathrm{D}} \:\alpha_{\mathrm{D}} \\ $$$$\Rightarrow\left\{\frac{\mathrm{r}}{\mathrm{R}−\mathrm{r}}×\left[\:\mathrm{I}_{\mathrm{B}} +\mathrm{m}\left(\mathrm{R}−\mathrm{r}\right)^{\mathrm{2}} \right]×\left[\mathrm{1}+\frac{\mathrm{R}^{\mathrm{2}} }{\mathrm{r}^{\mathrm{2}} }×\frac{\mathrm{I}_{\mathrm{D}} }{\mathrm{I}_{\mathrm{R}} }\right]+\left(\frac{\mathrm{R}}{\mathrm{r}}−\mathrm{1}\right)\mathrm{I}_{\mathrm{D}} \right\}\alpha_{\mathrm{D}} =−\left(\mathrm{m}+\frac{\mathrm{m}_{\mathrm{0}} }{\mathrm{2}}\right)\left(\mathrm{R}−\mathrm{r}\right)\mathrm{g} \\ $$$$\Rightarrow\:\alpha_{\mathrm{D}} =−\frac{\left(\mathrm{m}+\frac{\mathrm{m}_{\mathrm{0}} }{\mathrm{2}}\right)\left(\mathrm{R}−\mathrm{r}\right)\mathrm{g}}{\left[\:\frac{\mathrm{r}}{\mathrm{R}−\mathrm{r}}×\mathrm{I}_{\mathrm{B}} +\mathrm{mr}\left(\mathrm{R}−\mathrm{r}\right)\right]\left(\mathrm{1}+\frac{\mathrm{R}^{\mathrm{2}} }{\mathrm{r}^{\mathrm{2}} }×\frac{\mathrm{I}_{\mathrm{D}} }{\mathrm{I}_{\mathrm{R}} }\right)+\left(\frac{\mathrm{R}}{\mathrm{r}}−\mathrm{1}\right)\mathrm{I}_{\mathrm{D}} } \\ $$$$\Rightarrow\:\alpha_{\mathrm{B}} =−\frac{\mathrm{r}}{\mathrm{R}−\mathrm{r}}\left(\mathrm{1}+\frac{\mathrm{R}^{\mathrm{2}} }{\mathrm{r}^{\mathrm{2}} }×\frac{\mathrm{I}_{\mathrm{D}} }{\mathrm{I}_{\mathrm{R}} }\right)\alpha_{\mathrm{D}} \\ $$$$\Rightarrow\alpha_{\mathrm{R}} =\left(\mathrm{1}−\frac{\mathrm{r}}{\mathrm{R}}\right)\alpha_{\mathrm{B}} +\frac{\mathrm{r}}{\mathrm{R}}\alpha_{\mathrm{D}} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{R}=\mathrm{3r}\:\mathrm{and}\:\mathrm{M}=\mathrm{m}_{\mathrm{0}} =\mathrm{m},\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{I}_{\mathrm{R}} =\mathrm{MR}^{\mathrm{2}} =\mathrm{9mr}^{\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{D}} =\frac{\mathrm{mr}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{B}} =\frac{\mathrm{m}_{\mathrm{0}} \left(\mathrm{R}−\mathrm{r}\right)^{\mathrm{2}} }{\mathrm{3}}=\frac{\mathrm{4mr}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow\:\alpha_{\mathrm{D}} =−\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{g}}{\mathrm{r}}\:\:\left(\curvearrowleft\right)\:\mathrm{for}\:\mathrm{disc} \\ $$$$\Rightarrow\:\alpha_{\mathrm{B}} =\frac{\mathrm{9}}{\mathrm{20}}×\frac{\mathrm{g}}{\mathrm{r}}\:\:\left(\curvearrowright\right)\:\mathrm{for}\:\mathrm{rod} \\ $$$$\Rightarrow\alpha_{\mathrm{R}} =\frac{\mathrm{1}}{\mathrm{10}}×\frac{\mathrm{g}}{\mathrm{r}}\:\:\left(\curvearrowright\right)\:\mathrm{for}\:\mathrm{ring} \\ $$
Commented by mrW1 last updated on 01/Nov/17
Commented by ajfour last updated on 02/Nov/17

$$\:\boldsymbol{{your}}\:\boldsymbol{{answers}}\:\boldsymbol{{are}}\:\boldsymbol{{correct}}\: \\ $$$$\boldsymbol{{Sir}}. \\ $$$$\:{I}\:{checked}\:{your}\:{solution}, \\ $$$${carefully},\:{dint}\:{find}\:{any}\:{error}, \\ $$$${attempted}\:{on}\:{my}\:{own},\:{got}\:{the} \\ $$$${same}\:{answers}.\:\boldsymbol{\alpha}_{{D}} =−\frac{\mathrm{3}{g}}{\mathrm{5}{r}}\:. \\ $$$${Thank}\:{you}\:{Sir}. \\ $$
Commented by mrW1 last updated on 02/Nov/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{rechecking}! \\ $$
