Question Number 23559 by ajfour last updated on 01/Nov/17
Commented by ajfour last updated on 01/Nov/17

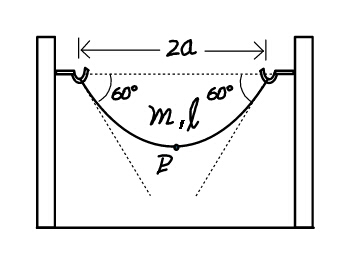
$${For}\:{the}\:{situation}\:{shown},\:{find}\: \\ $$$${the}\:\boldsymbol{{tension}}\:\boldsymbol{{T}}_{\mathrm{0}} \:{at}\:{midpoint}\:{P}. \\ $$$${Also}\:{find}\:{the}\:{length}\:\boldsymbol{{l}}\:{of}\:{rope}\:{in} \\ $$$${terms}\:{of}\:\boldsymbol{{a}}.\:{Given}\:{mass}\:{of}\:{rope} \\ $$$${is}\:\boldsymbol{{m}}.\:{Angle}\:{of}\:{rope}\:{with}\:{the} \\ $$$${horizontal}\:{is}\:\mathrm{60}°\:{at}\:{the}\:{ends}. \\ $$
Answered by mrW1 last updated on 01/Nov/17
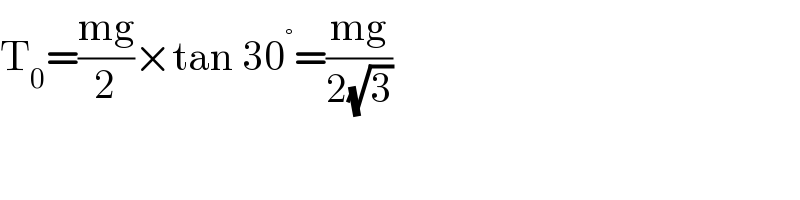
$$\mathrm{T}_{\mathrm{0}} =\frac{\mathrm{mg}}{\mathrm{2}}×\mathrm{tan}\:\mathrm{30}^{°} =\frac{\mathrm{mg}}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$
Commented by ajfour last updated on 02/Nov/17
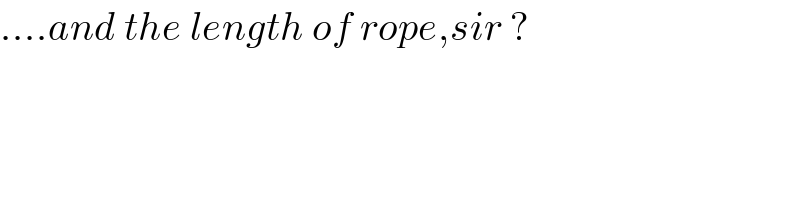
$$….{and}\:{the}\:{length}\:{of}\:{rope},{sir}\:? \\ $$
Commented by ajfour last updated on 01/Nov/17

$${Correct}\:{Sir}\:. \\ $$
Commented by mrW1 last updated on 02/Nov/17
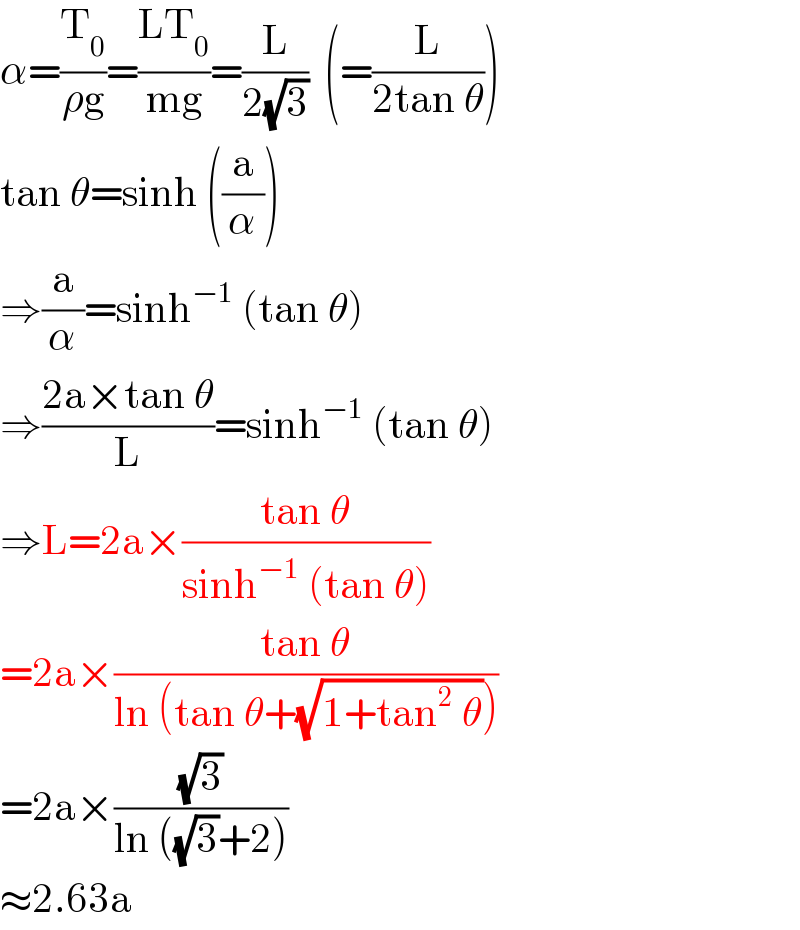
$$\alpha=\frac{\mathrm{T}_{\mathrm{0}} }{\rho\mathrm{g}}=\frac{\mathrm{LT}_{\mathrm{0}} }{\mathrm{mg}}=\frac{\mathrm{L}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\:\left(=\frac{\mathrm{L}}{\mathrm{2tan}\:\theta}\right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{sinh}\:\left(\frac{\mathrm{a}}{\alpha}\right) \\ $$$$\Rightarrow\frac{\mathrm{a}}{\alpha}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right) \\ $$$$\Rightarrow\frac{\mathrm{2a}×\mathrm{tan}\:\theta}{\mathrm{L}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right) \\ $$$$\Rightarrow\mathrm{L}=\mathrm{2a}×\frac{\mathrm{tan}\:\theta}{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)} \\ $$$$=\mathrm{2a}×\frac{\mathrm{tan}\:\theta}{\mathrm{ln}\:\left(\mathrm{tan}\:\theta+\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}\right)} \\ $$$$=\mathrm{2a}×\frac{\sqrt{\mathrm{3}}}{\mathrm{ln}\:\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)} \\ $$$$\approx\mathrm{2}.\mathrm{63a} \\ $$
Commented by ajfour last updated on 02/Nov/17

$$\:\:\boldsymbol{{l}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}\boldsymbol{{a}}}{\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}\:\:?? \\ $$
Commented by mrW1 last updated on 02/Nov/17

$$\mathrm{yes},\:\mathrm{with}\:\theta=\mathrm{60}°. \\ $$
Commented by ajfour last updated on 02/Nov/17

$${thank}\:{you}\:{Sir}. \\ $$
