Question Number 23897 by ajfour last updated on 09/Nov/17
Commented by ajfour last updated on 09/Nov/17

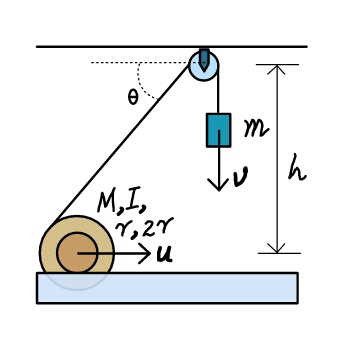
$$\:{The}\:{string}\:{is}\:{wrapped}\:{around} \\ $$$${the}\:{outer}\:{cicumference}\:{of}\:{spool} \\ $$$${of}\:{radius}\:\mathrm{2}{r}\:,\:{while}\:{it}\:{rolls}\:{on} \\ $$$${the}\:{track}\:{on}\:{its}\:{inner}\:{circle}\:{of} \\ $$$${radius}\:{r}.\:{Relate}\:\boldsymbol{{v}}\:{with}\:\boldsymbol{{u}}\:{in}\:{terms} \\ $$$${of}\:\theta,\:{r},\:{h},\:{M},\:{etc}.,\:{whichever} \\ $$$${necessary}. \\ $$
Commented by ajfour last updated on 09/Nov/17
![v = −s((d𝛗/dt))cos (𝛉−𝛗) ; u=−r((d𝛗/dt)) ; ssin 𝛗 =2rsin 𝛉 ; tan 𝛗 =((2rsin 𝛉)/(r(1+2cos 𝛉))) =((2sin θ)/(1+2cos θ)) so v=((u/r))scos (𝛉−φ) =u(((2sin 𝛉)/(sin 𝛗)))[cos 𝛉cos 𝛗+sin 𝛉sin 𝛗] =u(2sin 𝛉)[((cos 𝛉)/(tan 𝛗))+sin 𝛉] =2usin 𝛉(((cos 𝛉(1+2cos 𝛉))/(2sin 𝛉))+sin 𝛉) =u(2+cos 𝛉) .](https://www.tinkutara.com/question/Q23919.png)
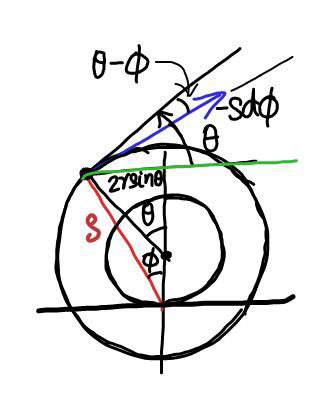
$$\boldsymbol{{v}}\:=\:−\boldsymbol{{s}}\left(\frac{\boldsymbol{{d}\phi}}{\boldsymbol{{dt}}}\right)\mathrm{cos}\:\left(\boldsymbol{\theta}−\boldsymbol{\phi}\right)\:\:;\:\: \\ $$$$\boldsymbol{{u}}=−\boldsymbol{{r}}\left(\frac{\boldsymbol{{d}\phi}}{\boldsymbol{{dt}}}\right)\:; \\ $$$$\:\:\boldsymbol{{s}}\mathrm{sin}\:\boldsymbol{\phi}\:=\mathrm{2}\boldsymbol{{r}}\mathrm{sin}\:\boldsymbol{\theta}\:\:; \\ $$$$\:\mathrm{tan}\:\boldsymbol{\phi}\:=\frac{\mathrm{2}\boldsymbol{{r}}\mathrm{sin}\:\boldsymbol{\theta}}{\boldsymbol{{r}}\left(\mathrm{1}+\mathrm{2cos}\:\boldsymbol{\theta}\right)}\:=\frac{\mathrm{2sin}\:\theta}{\mathrm{1}+\mathrm{2cos}\:\theta} \\ $$$$\boldsymbol{{so}}\:\:\:\:\:\boldsymbol{{v}}=\left(\frac{\boldsymbol{{u}}}{\boldsymbol{{r}}}\right)\boldsymbol{{s}}\mathrm{cos}\:\left(\boldsymbol{\theta}−\phi\right) \\ $$$$\:=\boldsymbol{{u}}\left(\frac{\mathrm{2sin}\:\boldsymbol{\theta}}{\mathrm{sin}\:\boldsymbol{\phi}}\right)\left[\mathrm{cos}\:\boldsymbol{\theta}\mathrm{cos}\:\boldsymbol{\phi}+\mathrm{sin}\:\boldsymbol{\theta}\mathrm{sin}\:\boldsymbol{\phi}\right] \\ $$$$\:=\boldsymbol{{u}}\left(\mathrm{2sin}\:\boldsymbol{\theta}\right)\left[\frac{\mathrm{cos}\:\boldsymbol{\theta}}{\mathrm{tan}\:\boldsymbol{\phi}}+\mathrm{sin}\:\boldsymbol{\theta}\right] \\ $$$$\:=\mathrm{2}\boldsymbol{{u}}\mathrm{sin}\:\boldsymbol{\theta}\left(\frac{\mathrm{cos}\:\boldsymbol{\theta}\left(\mathrm{1}+\mathrm{2cos}\:\boldsymbol{\theta}\right)}{\mathrm{2sin}\:\boldsymbol{\theta}}+\mathrm{sin}\:\boldsymbol{\theta}\right) \\ $$$$\:=\boldsymbol{{u}}\left(\mathrm{2}+\mathrm{cos}\:\boldsymbol{\theta}\right)\:. \\ $$
Commented by ajfour last updated on 09/Nov/17
Answered by Physics lover last updated on 10/Nov/17

$${r}\omega\:=\:{u}\:\Rightarrow\:\mathrm{2}{r}\omega=\:\mathrm{2}{u} \\ $$$$ \\ $$$${using}\:{rigid}\:{body}\:{constraint}. \\ $$$$\Rightarrow\:{v}\:=\:{u}\left(\mathrm{2}\:+\:{Cos}\:\theta\right) \\ $$$$ \\ $$$${assuming}\:{that}\:{the}\:{spool}\:{is}\: \\ $$$${purely}\:{rolling}\:{on}\:{the}\:{plank}, \\ $$$${plank}\:{is}\:{fixed},{neglecting}\:{gravity} \\ $$$${and}\:{string}\:{is}\:{ideal}. \\ $$$$ \\ $$
Commented by ajfour last updated on 09/Nov/17
$${Your}\:{answer}\:{is}\:{correct}\:. \\ $$
