Question Number 23920 by ajfour last updated on 09/Nov/17
Commented by ajfour last updated on 09/Nov/17

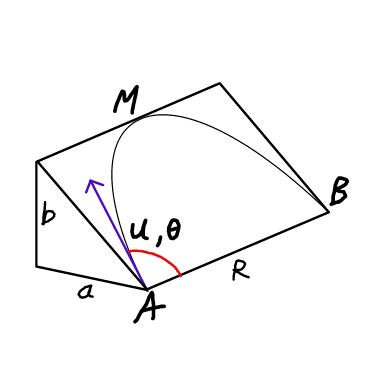
$${Find}\:\boldsymbol{{u}},\:\boldsymbol{\theta}\:{for}\:{a}\:{projecile}\:{in}\:{terms} \\ $$$${of}\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:{and}\:\boldsymbol{{R}}\:{such}\:{that}\:{it} \\ $$$${goes}\:{from}\:{A}\:{to}\:{B}\:{through}\:{M}\:, \\ $$$${the}\:{midpoint}\:{of}\:{upper}\:{edge}. \\ $$$${Assume}\:{the}\:{incline}\:{frictionless}. \\ $$
Answered by Physics lover last updated on 10/Nov/17
![x direction is along AB and y along (√(a^2 +b^2 )) ((height)/(range)) = ((tan θ)/4) ⇒ tan θ = ((4(√(a^2 +b^2 )))/R) H = (u_y ^2 /(2∙ ∣a_y ∣)) ⇒ ((u^2 Sin^2 θ)/(2g((b/( (√(a^2 +b^2 ))))))) = (√(a^2 +b^2 )) ⇒ u = (√((2gb)/({Sin^2 θ}))) = (√((2gb)/({((16(a^2 + b^2 ))/(16(a^2 +b^2 ) +R^2 ))}))) ⇒ u =(√((2gb[16(a^2 +b^2 )+R^2 ])/(16(a^2 +b^2 ))))](https://www.tinkutara.com/question/Q23927.png)
$${x}\:{direction}\:{is}\:{along}\:{AB} \\ $$$${and}\:{y}\:{along}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$ \\ $$$$\frac{{height}}{{range}}\:=\:\frac{{tan}\:\theta}{\mathrm{4}}\:\Rightarrow\:{tan}\:\theta\:=\:\frac{\mathrm{4}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{R}} \\ $$$$ \\ $$$${H}\:=\:\frac{{u}_{{y}} ^{\mathrm{2}} }{\mathrm{2}\centerdot\:\mid{a}_{{y}} \mid}\:\Rightarrow\:\frac{{u}^{\mathrm{2}} \:{Sin}\:^{\mathrm{2}} \:\theta}{\mathrm{2}{g}\left(\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)}\:=\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{u}\:=\:\sqrt{\frac{\mathrm{2}{gb}}{\left\{{Sin}^{\mathrm{2}} \:\theta\right\}}}\:=\:\sqrt{\frac{\mathrm{2}{gb}}{\left\{\frac{\mathrm{16}\left({a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \right)}{\mathrm{16}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\:+{R}^{\mathrm{2}} }\right\}}} \\ $$$$\Rightarrow\:{u}\:=\sqrt{\frac{\mathrm{2}{gb}\left[\mathrm{16}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{R}^{\mathrm{2}} \right]}{\mathrm{16}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}} \\ $$
Commented by ajfour last updated on 10/Nov/17
$${Very}\:{Nice}.\:{Thank}\:{you}. \\ $$
Commented by Physics lover last updated on 10/Nov/17
$${you}\:{are}\:{welcome},{sir}. \\ $$
