Question Number 23937 by ajfour last updated on 10/Nov/17
Commented by ajfour last updated on 10/Nov/17

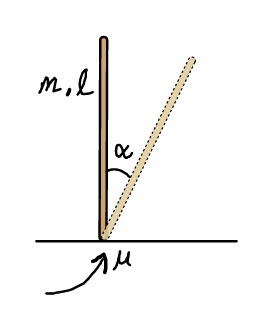
$${A}\:{thin}\:{rod}\:{placed}\:{perpendicular} \\ $$$${on}\:{a}\:{rough}\:{horizontal}\:{surface} \\ $$$${and}\:{released}\:{at}\:{rest}.\:{Find}\:{angle} \\ $$$$\boldsymbol{\alpha}\:{at}\:{which}\:{its}\:{bottom}\:{end}\:{starts} \\ $$$${slipping}.\:{The}\:{coefficient}\:{of} \\ $$$${friction}\:{for}\:{surface}\:{and}\:{rod}\:{is}\:\boldsymbol{\mu}. \\ $$
Answered by Physics lover last updated on 10/Nov/17
![assuming that the rod has turned by an angle θ and further θ + dθ α = ((mg Sin θ (l/2))/((ml^2 )/3)) ⇒ α = ((3g Sin θ)/(2l)) ...i ⇒ ω^(2 ) = ((3g (1−Cos θ))/l) .... ii mg − N = (mω^2 (l/2) Cos θ ) + ((3mgSin^2 θ)/4) ⇒ N = {mg − mω^(2 ) (l/2) Cos θ − ((3mg Sin^2 θ )/4) } ⇒ N = mg{ 1− (((3(1−Cos θ))/2))Cos θ −((3Sin^2 θ)/4)} ⇒ N = ((mg)/4) [4 − 6 Cos θ + 6 Cos^(2 ) θ −3 + 3 Cos^(2 ) θ ] ⇒ N = ((mg)/4)[ 1− 3 Cos θ ]^2 we can have two cases 1. when mg Cos θ > mω^2 (l/2) 2. mω^(2 ) (l/2) > mg Cos θ in first case μN Sin θ will be in opposite direction of mg Cos θ. ⇒mg Cos θ ± μ N Sine θ = mω^2 (l/2) ⇒mg Cos θ ± μ ((mg(1 − 3 Cos θ)^2 )/4)Sin θ = ((3mg(1− Cos θ))/2) ⇒4 Cos θ ± μ∙Sin θ ∙ (1− 3 Cos θ)^2 =6− 6 Cos θ ⇒10 Cos θ ± μ Sin θ(1− 3 Cos θ)^2 = 6 α = θ : it satisfies the above equation](https://www.tinkutara.com/question/Q23941.png)
$${assuming}\:{that}\:{the}\:{rod}\:{has}\:{turned}\:{by} \\ $$$${an}\:{angle}\:\theta\:{and}\:{further}\:\theta\:+\:{d}\theta \\ $$$$\alpha\:=\:\frac{{mg}\:{Sin}\:\theta\:\frac{{l}}{\mathrm{2}}}{\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}}\:\Rightarrow\:\alpha\:=\:\frac{\mathrm{3}{g}\:{Sin}\:\theta}{\mathrm{2}{l}}\:\:…{i} \\ $$$$\Rightarrow\:\omega\:^{\mathrm{2}\:} =\:\frac{\mathrm{3}{g}\:\left(\mathrm{1}−{Cos}\:\theta\right)}{{l}}\:\:\:\:\:….\:{ii} \\ $$$${mg}\:−\:{N}\:=\:\left({m}\omega^{\mathrm{2}} \frac{{l}}{\mathrm{2}}\:{Cos}\:\theta\:\right)\:+\:\frac{\mathrm{3}{mgSin}^{\mathrm{2}} \:\theta}{\mathrm{4}} \\ $$$$\Rightarrow\:{N}\:=\:\left\{{mg}\:−\:{m}\omega^{\mathrm{2}\:} \frac{{l}}{\mathrm{2}}\:{Cos}\:\theta\:\:−\:\frac{\mathrm{3}{mg}\:{Sin}^{\mathrm{2}} \:\theta\:}{\mathrm{4}}\:\right\}\:\:\: \\ $$$$\Rightarrow\:{N}\:=\:{mg}\left\{\:\mathrm{1}−\:\left(\frac{\mathrm{3}\left(\mathrm{1}−{Cos}\:\theta\right)}{\mathrm{2}}\right){Cos}\:\theta\:−\frac{\mathrm{3}{Sin}^{\mathrm{2}} \:\theta}{\mathrm{4}}\right\} \\ $$$$\Rightarrow\:{N}\:=\:\frac{{mg}}{\mathrm{4}}\:\left[\mathrm{4}\:−\:\mathrm{6}\:{Cos}\:\theta\:+\:\mathrm{6}\:{Cos}\:^{\mathrm{2}\:} \theta\:−\mathrm{3}\:+\:\mathrm{3}\:{Cos}\:^{\mathrm{2}\:} \theta\:\right] \\ $$$$\Rightarrow\:{N}\:=\:\frac{{mg}}{\mathrm{4}}\left[\:\mathrm{1}−\:\mathrm{3}\:{Cos}\:\theta\:\right]^{\mathrm{2}} \\ $$$${we}\:{can}\:{have}\:{two}\:{cases} \\ $$$$\mathrm{1}.\:{when}\:{mg}\:{Cos}\:\theta\:>\:{m}\omega^{\mathrm{2}} \frac{{l}}{\mathrm{2}} \\ $$$$\mathrm{2}.\:\:{m}\omega^{\mathrm{2}\:} \frac{{l}}{\mathrm{2}}\:>\:{mg}\:{Cos}\:\theta \\ $$$${in}\:{first}\:{case}\:\mu{N}\:{Sin}\:\theta\:{will}\:{be}\:{in} \\ $$$${opposite}\:{direction}\:{of}\:{mg}\:{Cos}\:\theta. \\ $$$$ \\ $$$$\Rightarrow{mg}\:{Cos}\:\theta\:\pm\:\mu\:{N}\:{Sine}\:\theta\:=\:{m}\omega^{\mathrm{2}} \:\frac{{l}}{\mathrm{2}} \\ $$$$\Rightarrow{mg}\:{Cos}\:\theta\:\pm\:\mu\:\frac{{mg}\left(\mathrm{1}\:−\:\mathrm{3}\:{Cos}\:\theta\right)^{\mathrm{2}} }{\mathrm{4}}{Sin}\:\theta\:=\:\frac{\mathrm{3}{mg}\left(\mathrm{1}−\:{Cos}\:\theta\right)}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}\:{Cos}\:\theta\:\pm\:\mu\centerdot{Sin}\:\theta\:\centerdot\:\left(\mathrm{1}−\:\mathrm{3}\:{Cos}\:\:\theta\right)^{\mathrm{2}} =\mathrm{6}−\:\mathrm{6}\:{Cos}\:\theta \\ $$$$\Rightarrow\mathrm{10}\:{Cos}\:\theta\:\pm\:\mu\:{Sin}\:\theta\left(\mathrm{1}−\:\mathrm{3}\:{Cos}\:\theta\right)^{\mathrm{2}} \:=\:\mathrm{6} \\ $$$$\alpha\:=\:\theta\::\:{it}\:{satisfies}\:{the}\:{above}\:{equation} \\ $$$$ \\ $$
Commented by ajfour last updated on 10/Nov/17
![mg−N = mω^2 (l/2)cos θ+((mαl)/2)sin θ ⇒ mg−N=((3mgcos θ(1−cos θ))/2) + ((3mg)/4)sin^2 θ ⇒ N=mg[1−(3/2)cos θ(1−cos θ) −(3/4)sin^2 θ ] N = ((mg)/4)[4−6cos θ+6cos^2 θ−3sin^2 θ] =((mg)/4)(1−6cos θ+9cos^2 θ) N=((mg)/4)(3cos 𝛉−1)^2 ⇒ N is zero for θ=cos^(−1) ((1/3)) . If f ≥ 𝛍N for θ < cos^(−1) ((1/3)) then slipping occurs at a lesser angle. f =m(((𝛂l)/2)cos 𝛉−((𝛚^2 l)/2)sin 𝛉) =((3mg)/4)sin θcos θ−((3mg)/2)sin θ(1−cos θ) =((3mg)/4)sin θ[cos θ−2+2cos θ] =((3mg)/4)sin θ(3cos θ−2) f > 𝛍N ⇒ ((3mg)/4)sin θ(3cos θ−2) > ((μmg)/4)(3cos θ−1)^2 or 𝛍 < ((3sin θ(3cos θ−2))/((3cos θ−1)^2 )) So if slipping doesn′t take place till θ ≤ cos^(−1) ((1/3)) , contact itself breaks at θ=cos^(−1) ((1/3)) ; and for slipping to occur at a lesser angle, 𝛉 should be such that ((sin θ(cos θ−(2/3)))/((cos θ−(1/3))^2 )) > μ .](https://www.tinkutara.com/question/Q23942.png)
$${mg}−{N}\:=\:{m}\omega^{\mathrm{2}} \frac{{l}}{\mathrm{2}}\mathrm{cos}\:\theta+\frac{{m}\alpha{l}}{\mathrm{2}}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:{mg}−{N}=\frac{\mathrm{3}{mg}\mathrm{cos}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\frac{\mathrm{3}{mg}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:{N}={mg}\left[\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \theta\:\right] \\ $$$$\boldsymbol{{N}}\:=\:\frac{{mg}}{\mathrm{4}}\left[\mathrm{4}−\mathrm{6cos}\:\theta+\mathrm{6cos}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:^{\mathrm{2}} \theta\right] \\ $$$$\:\:=\frac{{mg}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{6cos}\:\theta+\mathrm{9cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\boldsymbol{{N}}=\frac{\boldsymbol{{mg}}}{\mathrm{4}}\left(\mathrm{3cos}\:\boldsymbol{\theta}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{N}\:{is}\:\:{zero}\:{for}\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:. \\ $$$${If}\:\boldsymbol{{f}}\:\geqslant\:\boldsymbol{\mu{N}}\:\:{for}\:\theta\:<\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:{then} \\ $$$${slipping}\:{occurs}\:{at}\:{a}\:{lesser}\:{angle}. \\ $$$$\boldsymbol{{f}}\:=\boldsymbol{{m}}\left(\frac{\boldsymbol{\alpha{l}}}{\mathrm{2}}\mathrm{cos}\:\boldsymbol{\theta}−\frac{\boldsymbol{\omega}^{\mathrm{2}} \boldsymbol{{l}}}{\mathrm{2}}\mathrm{sin}\:\boldsymbol{\theta}\right) \\ $$$$\:\:=\frac{\mathrm{3}{mg}}{\mathrm{4}}\mathrm{sin}\:\theta\mathrm{cos}\:\theta−\frac{\mathrm{3}{mg}}{\mathrm{2}}\mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\:=\frac{\mathrm{3}{mg}}{\mathrm{4}}\mathrm{sin}\:\theta\left[\mathrm{cos}\:\theta−\mathrm{2}+\mathrm{2cos}\:\theta\right] \\ $$$$\:=\frac{\mathrm{3}{mg}}{\mathrm{4}}\mathrm{sin}\:\theta\left(\mathrm{3cos}\:\theta−\mathrm{2}\right) \\ $$$$\boldsymbol{{f}}\:>\:\boldsymbol{\mu{N}}\:\:\:\Rightarrow \\ $$$$\frac{\mathrm{3}{mg}}{\mathrm{4}}\mathrm{sin}\:\theta\left(\mathrm{3cos}\:\theta−\mathrm{2}\right)\:>\:\frac{\mu{mg}}{\mathrm{4}}\left(\mathrm{3cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${or}\:\:\boldsymbol{\mu}\:<\:\frac{\mathrm{3sin}\:\theta\left(\mathrm{3cos}\:\theta−\mathrm{2}\right)}{\left(\mathrm{3cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:{So}\:{if}\:{slipping}\:{doesn}'{t}\:{take}\:{place} \\ $$$${till}\:\theta\:\leqslant\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:,\:{contact}\:{itself} \\ $$$${breaks}\:{at}\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:; \\ $$$${and}\:{for}\:{slipping} \\ $$$${to}\:{occur}\:{at}\:{a}\:{lesser}\:{angle},\:\:\boldsymbol{\theta} \\ $$$${should}\:{be}\:{such}\:{that} \\ $$$$\:\:\:\frac{\mathrm{sin}\:\theta\left(\mathrm{cos}\:\theta−\frac{\mathrm{2}}{\mathrm{3}}\right)}{\left(\mathrm{cos}\:\theta−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\:>\:\mu\:. \\ $$
Commented by Physics lover last updated on 10/Nov/17
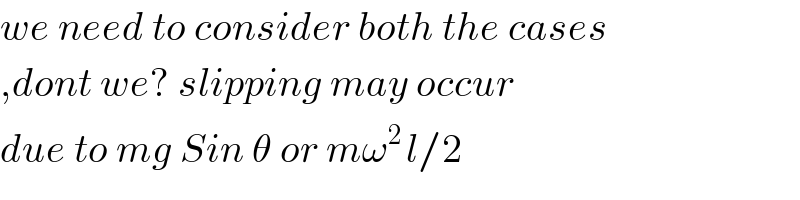
$${we}\:{need}\:{to}\:{consider}\:{both}\:{the}\:{cases} \\ $$$$,{dont}\:{we}?\:{slipping}\:{may}\:{occur} \\ $$$${due}\:{to}\:{mg}\:{Sin}\:\theta\:{or}\:{m}\omega^{\mathrm{2}\:} {l}/\mathrm{2} \\ $$
Commented by Physics lover last updated on 10/Nov/17
$${Is}\:{my}\:{answer}\:{correct}? \\ $$
Commented by ajfour last updated on 10/Nov/17
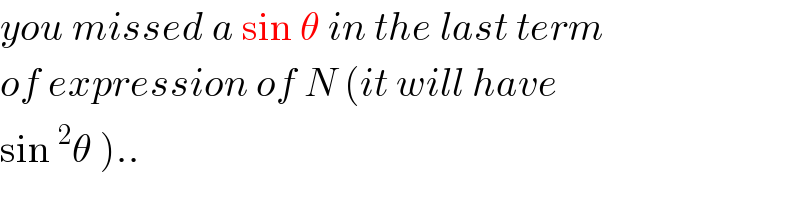
$${you}\:{missed}\:{a}\:\mathrm{sin}\:\theta\:{in}\:{the}\:{last}\:{term} \\ $$$${of}\:{expression}\:{of}\:{N}\:\left({it}\:{will}\:{have}\right. \\ $$$$\left.\mathrm{sin}\:^{\mathrm{2}} \theta\:\right).. \\ $$
Commented by Physics lover last updated on 10/Nov/17

$${yes}\:{sir}\:{its}\:{Sin}^{\mathrm{2}} \theta \\ $$
Commented by Physics lover last updated on 10/Nov/17
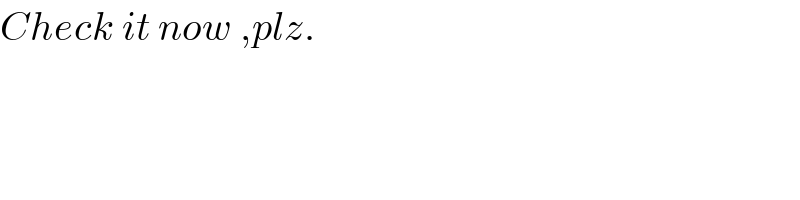
$${Check}\:{it}\:{now}\:,{plz}. \\ $$
Commented by Physics lover last updated on 10/Nov/17
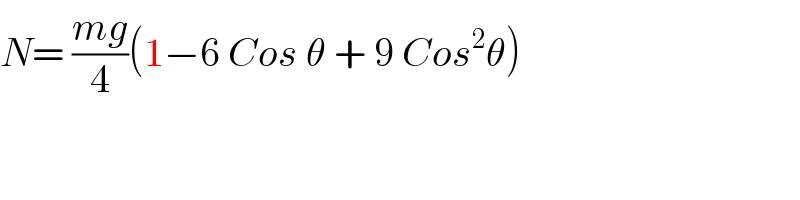
$${N}=\:\frac{{mg}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{6}\:{Cos}\:\theta\:+\:\mathrm{9}\:{Cos}^{\mathrm{2}} \theta\right) \\ $$
Commented by mrW1 last updated on 10/Nov/17
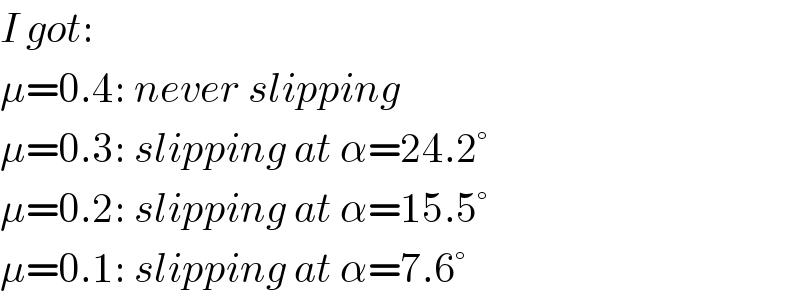
$${I}\:{got}: \\ $$$$\mu=\mathrm{0}.\mathrm{4}:\:{never}\:{slipping} \\ $$$$\mu=\mathrm{0}.\mathrm{3}:\:{slipping}\:{at}\:\alpha=\mathrm{24}.\mathrm{2}° \\ $$$$\mu=\mathrm{0}.\mathrm{2}:\:{slipping}\:{at}\:\alpha=\mathrm{15}.\mathrm{5}° \\ $$$$\mu=\mathrm{0}.\mathrm{1}:\:{slipping}\:{at}\:\alpha=\mathrm{7}.\mathrm{6}° \\ $$
Commented by Physics lover last updated on 10/Nov/17
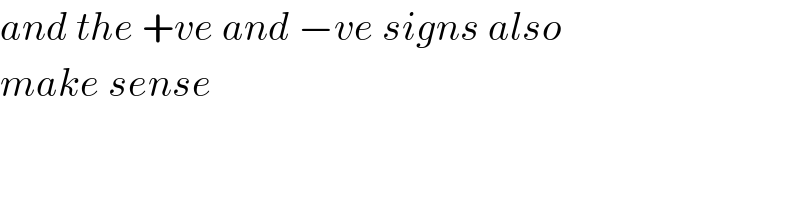
$${and}\:{the}\:+{ve}\:{and}\:−{ve}\:{signs}\:{also} \\ $$$${make}\:{sense} \\ $$
Commented by ajfour last updated on 10/Nov/17

$${yes}\:{MrW}\mathrm{1}\:{sir},\:{my}\:\:{corrected}\:{results} \\ $$$${predict}\:{the}\:{same}\:{pecific}\:{values}. \\ $$$${Thank}\:{you}\:{so}\:{much},\:{Sir}. \\ $$$${Thank}\:{you}\:{Physics}\:{lover}\: \\ $$$${for}\:{your}\:{cooperation}. \\ $$
Commented by Physics lover last updated on 10/Nov/17
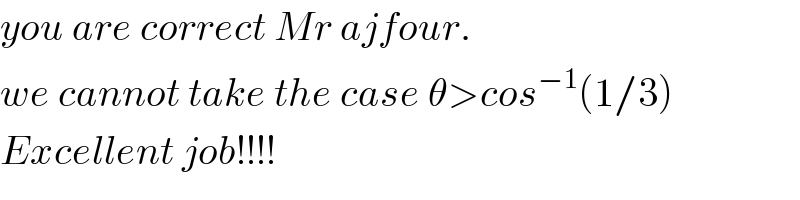
$${you}\:{are}\:{correct}\:{Mr}\:{ajfour}. \\ $$$${we}\:{cannot}\:{take}\:{the}\:{case}\:\theta>{cos}^{−\mathrm{1}} \left(\mathrm{1}/\mathrm{3}\right) \\ $$$${Excellent}\:{job}!!!! \\ $$
Commented by Physics lover last updated on 10/Nov/17
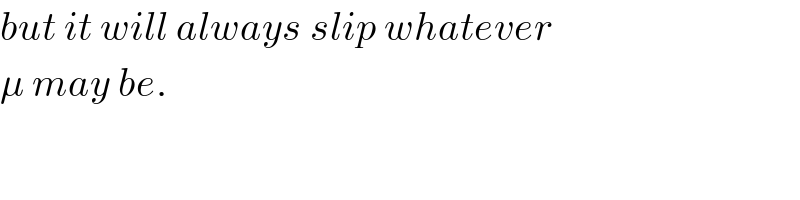
$${but}\:{it}\:{will}\:{always}\:{slip}\:{whatever} \\ $$$$\mu\:{may}\:{be}. \\ $$
Commented by mrW1 last updated on 10/Nov/17
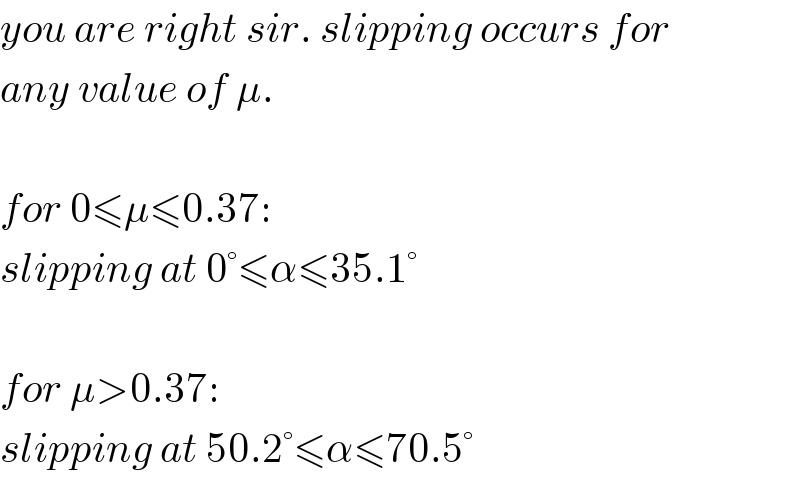
$${you}\:{are}\:{right}\:{sir}.\:{slipping}\:{occurs}\:{for} \\ $$$${any}\:{value}\:{of}\:\mu. \\ $$$$ \\ $$$${for}\:\mathrm{0}\leqslant\mu\leqslant\mathrm{0}.\mathrm{37}: \\ $$$${slipping}\:{at}\:\mathrm{0}°\leqslant\alpha\leqslant\mathrm{35}.\mathrm{1}° \\ $$$$ \\ $$$${for}\:\mu>\mathrm{0}.\mathrm{37}: \\ $$$${slipping}\:{at}\:\mathrm{50}.\mathrm{2}°\leqslant\alpha\leqslant\mathrm{70}.\mathrm{5}° \\ $$
Commented by mrW1 last updated on 10/Nov/17
Commented by Physics lover last updated on 10/Nov/17
Commented by Physics lover last updated on 10/Nov/17

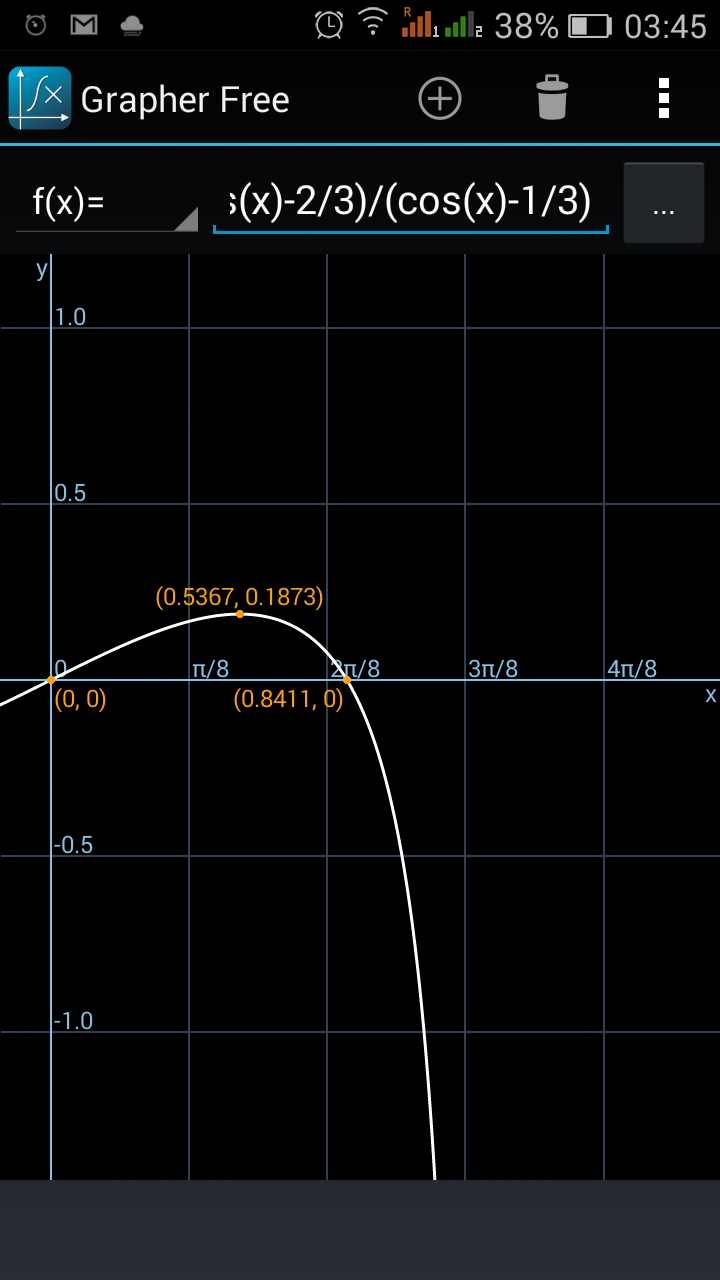
$${there}\:{is}\:{some}\:{problem}.{At}\:\theta\:=\:\mathrm{0}.\mathrm{8411} \\ $$$$\Rightarrow\mu=\mathrm{0}\Rightarrow\:{it}\:{will}\:{slip}\:{at}\:{that}\:{point}. \\ $$$${which}\:{is}\:{not}\:{true}. \\ $$$$\Rightarrow\:{the}\:\mu\:{which}\:{we}\:{are}\:{calculaing} \\ $$$${is}\:{for}\:{a}\:{given}\:\theta. \\ $$$${i}\:{mean}\:,{if}\:{we}\:{want}\:{to}\:{start} \\ $$$${slipping}\:{at}\:\mathrm{0}.\mathrm{841}\Rightarrow\:\mu\:=\:\mathrm{0}.\mathrm{1873} \\ $$$${B}'{cuz}\:\mathrm{0}.\mathrm{5367}\:{will}\:{have}\:{to}\:{be} \\ $$$${covered}\:{before}\:\mathrm{0}.\mathrm{841}. \\ $$$${And}\:{it} \\ $$$${is}\:\mathrm{2}\:{for}\:\pi/\mathrm{2}\:.{but} \\ $$$${according}\:{to}\:{the}\:{following}\:{calculationd}\: \\ $$$${it}\:{should}\:{be}\:\mathrm{6}. \\ $$
Commented by Physics lover last updated on 10/Nov/17
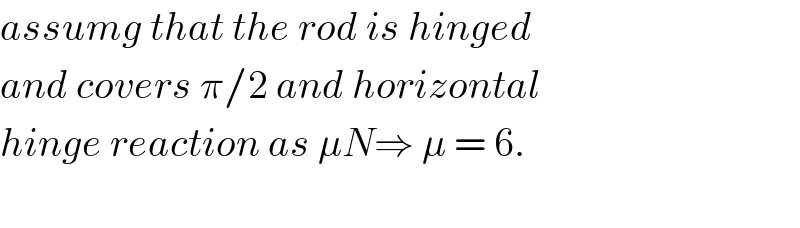
$${assumg}\:{that}\:{the}\:{rod}\:{is}\:{hinged} \\ $$$${and}\:{covers}\:\pi/\mathrm{2}\:{and}\:{horizontal} \\ $$$${hinge}\:{reaction}\:{as}\:\mu{N}\Rightarrow\:\mu\:=\:\mathrm{6}. \\ $$$$ \\ $$
Commented by mrW1 last updated on 11/Nov/17
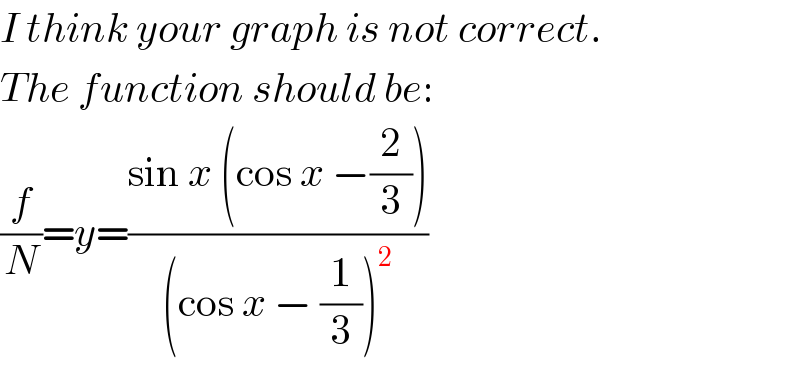
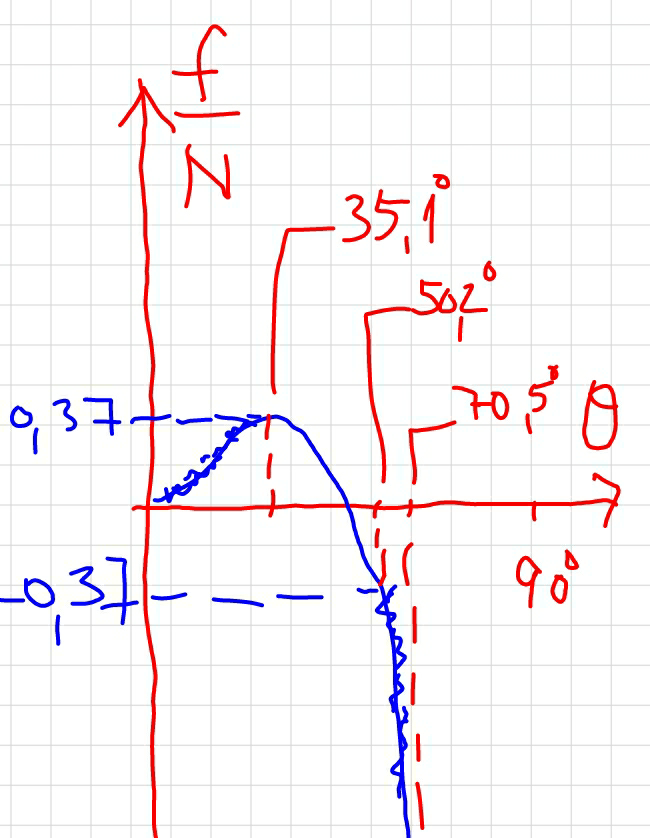
$${I}\:{think}\:{your}\:{graph}\:{is}\:{not}\:{correct}. \\ $$$${The}\:{function}\:{should}\:{be}: \\ $$$$\frac{{f}}{{N}}={y}=\frac{\mathrm{sin}\:{x}\:\left(\mathrm{cos}\:{x}\:−\frac{\mathrm{2}}{\mathrm{3}}\right)}{\left(\mathrm{cos}\:{x}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$
Commented by mrW1 last updated on 10/Nov/17
Commented by mrW1 last updated on 11/Nov/17
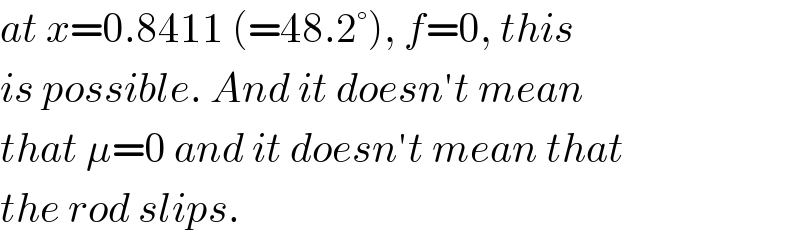
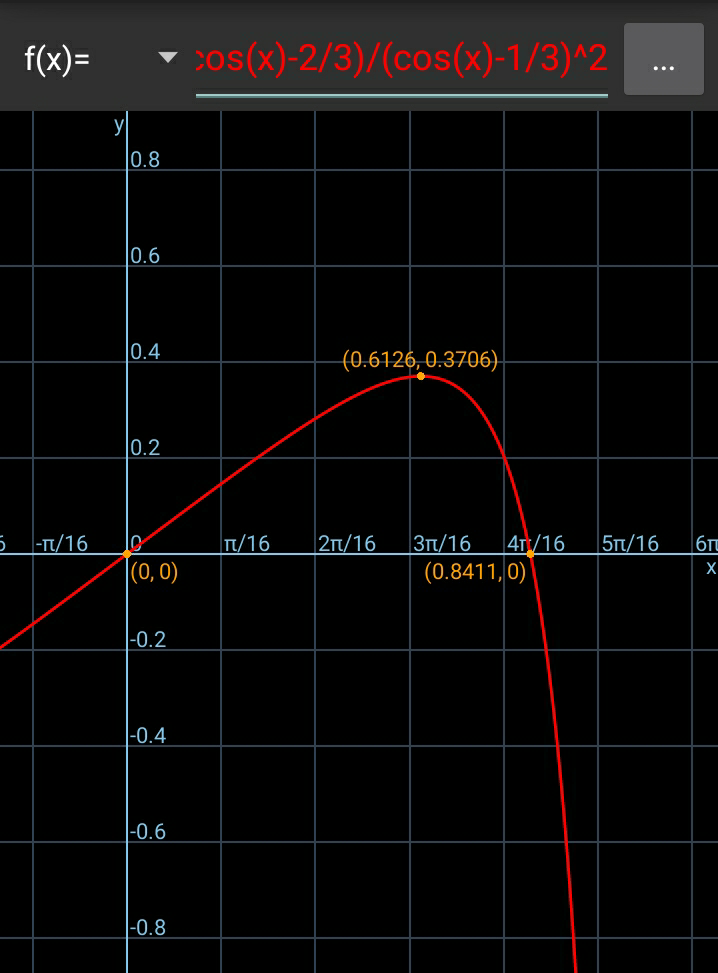
$${at}\:{x}=\mathrm{0}.\mathrm{8411}\:\left(=\mathrm{48}.\mathrm{2}°\right),\:{f}=\mathrm{0},\:{this} \\ $$$${is}\:{possible}.\:{And}\:{it}\:{doesn}'{t}\:{mean} \\ $$$${that}\:\mu=\mathrm{0}\:{and}\:{it}\:{doesn}'{t}\:{mean}\:{that} \\ $$$${the}\:{rod}\:{slips}. \\ $$
Commented by mrW1 last updated on 11/Nov/17
Commented by mrW1 last updated on 11/Nov/17

$${My}\:{opinion}\:{is}\:{that}\:{slipping}\:{always} \\ $$$${occur}\:{at}\:{an}\:{angle}\:{less}\:{than}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\approx\mathrm{70}.\mathrm{5}°\right). \\ $$$$ \\ $$$${If}\:\mu\leqslant\mathrm{0}.\mathrm{3706},\:{the}\:{angle}\:\alpha\:{at}\:{which} \\ $$$${the}\:{rod}\:{begins}\:{to}\:{slip}\:{fulfills} \\ $$$$\frac{\mathrm{sin}\:\alpha\:\left(\mathrm{cos}\:\alpha−\frac{\mathrm{2}}{\mathrm{3}}\right)}{\left(\mathrm{cos}\:\alpha−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }=\mu \\ $$$${and}\:\mathrm{0}\leqslant\alpha\leqslant\mathrm{35}.\mathrm{1}° \\ $$$$ \\ $$$${If}\:\mu>\mathrm{0}.\mathrm{3706},\:{the}\:{angle}\:\alpha\:{at}\:{which} \\ $$$${the}\:{rod}\:{begins}\:{to}\:{slip}\:{fulfills} \\ $$$$\frac{\mathrm{sin}\:\alpha\:\left(\mathrm{cos}\:\alpha−\frac{\mathrm{2}}{\mathrm{3}}\right)}{\left(\mathrm{cos}\:\alpha−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }=−\mu \\ $$$${and}\:\mathrm{50}.\mathrm{2}°<\alpha<\mathrm{70}.\mathrm{5}° \\ $$
Commented by mrW1 last updated on 11/Nov/17
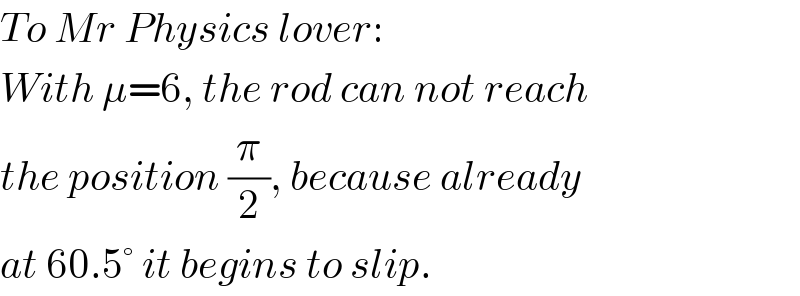
$${To}\:{Mr}\:{Physics}\:{lover}: \\ $$$${With}\:\mu=\mathrm{6},\:{the}\:{rod}\:{can}\:{not}\:{reach} \\ $$$${the}\:{position}\:\frac{\pi}{\mathrm{2}},\:{because}\:{already} \\ $$$${at}\:\mathrm{60}.\mathrm{5}°\:{it}\:{begins}\:{to}\:{slip}. \\ $$
Commented by ajfour last updated on 11/Nov/17

$${thank}\:{you}\:{Sir}.\:{This}\:{is}\:{finally} \\ $$$${very}\:{satisfactory}. \\ $$$${before}\:\theta\:{becomes}\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$${rod}\:{slips}\:{if}\:\mu\:{happens}\:{to}\:{be} \\ $$$${less}\:{than}\:{some}\:{calculable}\:{value} \\ $$$$\left(\mathrm{0}.\mathrm{37}\:{as}\:{shown}\:{in}\:{your}\:{graph}\:{post}\right) \\ $$$${and}\:{if}\:{it}\:{escapes}\:{slipping}\:{here}\:{at} \\ $$$${this}\:{angle}\:{then}\:{at}\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$${N}=\frac{{mg}}{\mathrm{4}}\:{while}\:{friction}\:{need}\:{not} \\ $$$${act}\:\left({is}\:{zero}\right).\:{But}\:{as}\:{angle}\:{grows} \\ $$$${beyond}\:{this}\:{friction}\:{reverses} \\ $$$${direction}\:{and}\:{grows}.\:{Normal} \\ $$$${force}\:{must}\:{be}\:{decreasing}\:{and} \\ $$$${becomes}\:{zero}\:{at}\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right). \\ $$$${No}\:{value}\:{of}\:\mu\:{can}\:{prevent}\: \\ $$$${slipping}\:{by}\:{this}\:{time}\:\left({for}\:{this}\right. \\ $$$$\left.{case}\right)\:{so}\:{for}\:{some}\:{given}\:{value} \\ $$$${of}\:\mu>\mathrm{0}.\mathrm{37}\:{rod}\:{slips}\:{for}\: \\ $$$$\:\:\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:<\:\alpha\:<\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:; \\ $$$${while}\:{if}\:\mu<\:\mathrm{0}.\mathrm{37}\:{it}\:{slips}\:{way} \\ $$$${before}\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:. \\ $$$$\left({This}\:{is}\:{my}\:{conclusion}\:{Sir},\right. \\ $$$$\left.{because}\:{of}\:{your}\:{kind}\:{efforts}\:.\right) \\ $$$$\:\mathcal{T}{hank}\:{you}\:{Sir}. \\ $$$$ \\ $$
Commented by Physics lover last updated on 11/Nov/17

$${hmmm}.{finally}. \\ $$
