Menu Close

Question-24078

Tinku Tara 0 Comments
Pin




Question Number 24078 by math solver last updated on 12/Nov/17
Commented by math solver last updated on 12/Nov/17
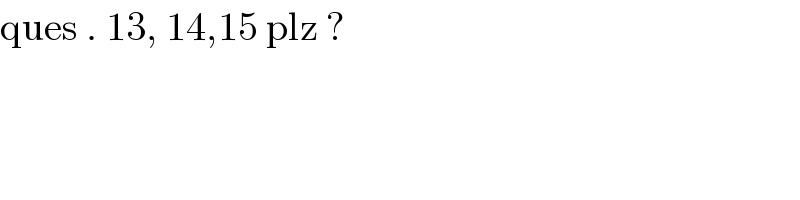
ques . 13, 14,15 plz ?
$$\mathrm{ques}\:.\:\mathrm{13},\:\mathrm{14},\mathrm{15}\:\mathrm{plz}\:? \\ $$
Commented by mrW1 last updated on 12/Nov/17
answers given are not visible.
$${answers}\:{given}\:{are}\:{not}\:{visible}. \\ $$
Commented by ajfour last updated on 12/Nov/17
(13) . −dT =μ[2Tsin ((dθ/2))] ⇒ ∫_T_2 ^( T) (dT/T) = −∫_0 ^( θ) μdθ T=T_2 e^(−μθ) ⇒ (T_2 /T_1 ) = e^(𝛍𝛑) .
$$\left(\mathrm{13}\right)\:. \\ $$$$\:\:\:−{dT}\:=\mu\left[\mathrm{2}{T}\mathrm{sin}\:\left(\frac{{d}\theta}{\mathrm{2}}\right)\right] \\ $$$$\Rightarrow\:\:\int_{{T}_{\mathrm{2}} } ^{\:\:{T}} \:\frac{{dT}}{{T}}\:=\:−\int_{\mathrm{0}} ^{\:\:\theta} \mu{d}\theta \\ $$$$\:\:{T}={T}_{\mathrm{2}} {e}^{−\mu\theta} \\ $$$$\Rightarrow\:\:\:\:\:\frac{\boldsymbol{{T}}_{\mathrm{2}} }{\boldsymbol{{T}}_{\mathrm{1}} }\:=\:\boldsymbol{{e}}^{\boldsymbol{\mu\pi}} \:. \\ $$
Commented by math solver last updated on 12/Nov/17
Commented by math solver last updated on 12/Nov/17
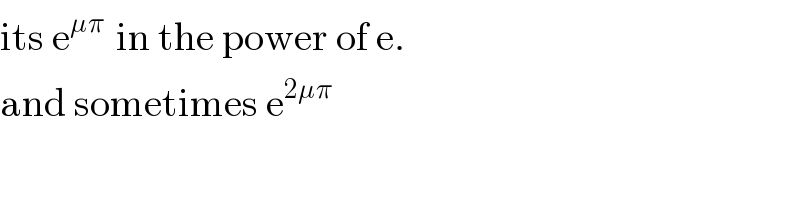
its e^(μπ ) in the power of e. and sometimes e^(2μπ)
$$\mathrm{its}\:\mathrm{e}^{\mu\pi\:} \:\mathrm{in}\:\mathrm{the}\:\mathrm{power}\:\mathrm{of}\:\mathrm{e}. \\ $$$$\mathrm{and}\:\mathrm{sometimes}\:\mathrm{e}^{\mathrm{2}\mu\pi} \\ $$
Commented by math solver last updated on 12/Nov/17
god bless you sir!
$$\mathrm{god}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}! \\ $$
Commented by ajfour last updated on 12/Nov/17
Answered by mrW1 last updated on 12/Nov/17
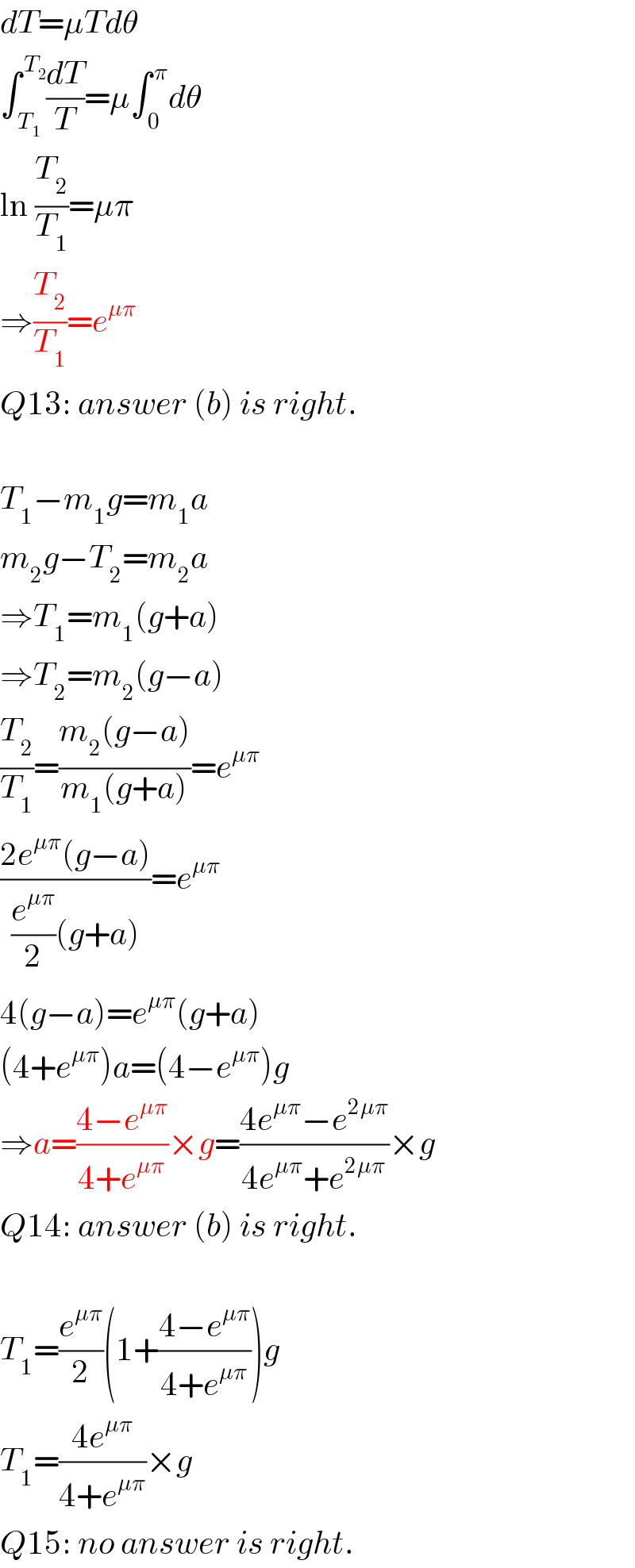
dT=μTdθ ∫_( T_1 ) ^( T_2 ) (dT/T)=μ∫_( 0) ^( π) dθ ln (T_2 /T_1 )=μπ ⇒(T_2 /T_1 )=e^(μπ) Q13: answer (b) is right. T_1 −m_1 g=m_1 a m_2 g−T_2 =m_2 a ⇒T_1 =m_1 (g+a) ⇒T_2 =m_2 (g−a) (T_2 /T_1 )=((m_2 (g−a))/(m_1 (g+a)))=e^(μπ) ((2e^(μπ) (g−a))/((e^(μπ) /2)(g+a)))=e^(μπ) 4(g−a)=e^(μπ) (g+a) (4+e^(μπ) )a=(4−e^(μπ) )g ⇒a=((4−e^(μπ) )/(4+e^(μπ) ))×g=((4e^(μπ) −e^(2μπ) )/(4e^(μπ) +e^(2μπ) ))×g Q14: answer (b) is right. T_1 =(e^(μπ) /2)(1+((4−e^(μπ) )/(4+e^(μπ) )))g T_1 =((4e^(μπ) )/(4+e^(μπ) ))×g Q15: no answer is right.
$${dT}=\mu{Td}\theta \\ $$$$\int_{\:{T}_{\mathrm{1}} } ^{\:{T}_{\mathrm{2}} } \frac{{dT}}{{T}}=\mu\int_{\:\mathrm{0}} ^{\:\pi} {d}\theta \\ $$$$\mathrm{ln}\:\frac{{T}_{\mathrm{2}} }{{T}_{\mathrm{1}} }=\mu\pi \\ $$$$\Rightarrow\frac{{T}_{\mathrm{2}} }{{T}_{\mathrm{1}} }={e}^{\mu\pi} \\ $$$${Q}\mathrm{13}:\:{answer}\:\left({b}\right)\:{is}\:{right}. \\ $$$$ \\ $$$${T}_{\mathrm{1}} −{m}_{\mathrm{1}} {g}={m}_{\mathrm{1}} {a} \\ $$$${m}_{\mathrm{2}} {g}−{T}_{\mathrm{2}} ={m}_{\mathrm{2}} {a} \\ $$$$\Rightarrow{T}_{\mathrm{1}} ={m}_{\mathrm{1}} \left({g}+{a}\right) \\ $$$$\Rightarrow{T}_{\mathrm{2}} ={m}_{\mathrm{2}} \left({g}−{a}\right) \\ $$$$\frac{{T}_{\mathrm{2}} }{{T}_{\mathrm{1}} }=\frac{{m}_{\mathrm{2}} \left({g}−{a}\right)}{{m}_{\mathrm{1}} \left({g}+{a}\right)}={e}^{\mu\pi} \\ $$$$\frac{\mathrm{2}{e}^{\mu\pi} \left({g}−{a}\right)}{\frac{{e}^{\mu\pi} }{\mathrm{2}}\left({g}+{a}\right)}={e}^{\mu\pi} \\ $$$$\mathrm{4}\left({g}−{a}\right)={e}^{\mu\pi} \left({g}+{a}\right) \\ $$$$\left(\mathrm{4}+{e}^{\mu\pi} \right){a}=\left(\mathrm{4}−{e}^{\mu\pi} \right){g} \\ $$$$\Rightarrow{a}=\frac{\mathrm{4}−{e}^{\mu\pi} }{\mathrm{4}+{e}^{\mu\pi} }×{g}=\frac{\mathrm{4}{e}^{\mu\pi} −{e}^{\mathrm{2}\mu\pi} }{\mathrm{4}{e}^{\mu\pi} +{e}^{\mathrm{2}\mu\pi} }×{g} \\ $$$${Q}\mathrm{14}:\:{answer}\:\left({b}\right)\:{is}\:{right}. \\ $$$$ \\ $$$${T}_{\mathrm{1}} =\frac{{e}^{\mu\pi} }{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{4}−{e}^{\mu\pi} }{\mathrm{4}+{e}^{\mu\pi} }\right){g} \\ $$$${T}_{\mathrm{1}} =\frac{\mathrm{4}{e}^{\mu\pi} }{\mathrm{4}+{e}^{\mu\pi} }×{g} \\ $$$${Q}\mathrm{15}:\:{no}\:{answer}\:{is}\:{right}. \\ $$
Commented by math solver last updated on 12/Nov/17
sir , can u plz elaborate your very 1st step. and how you took the limits :′ ....? You are correct ! god bless you sir.
$$\mathrm{sir}\:,\:\mathrm{can}\:\mathrm{u}\:\mathrm{plz}\:\mathrm{elaborate}\:\mathrm{your}\:\mathrm{very}\:\mathrm{1st}\:\mathrm{step}. \\ $$$$\mathrm{and}\:\mathrm{how}\:\mathrm{you}\:\mathrm{took}\:\mathrm{the}\:\mathrm{limits}\::'\:….? \\ $$$$\mathrm{You}\:\mathrm{are}\:\mathrm{correct}\:! \\ $$$$\mathrm{god}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mrW1 last updated on 12/Nov/17
Commented by mrW1 last updated on 12/Nov/17
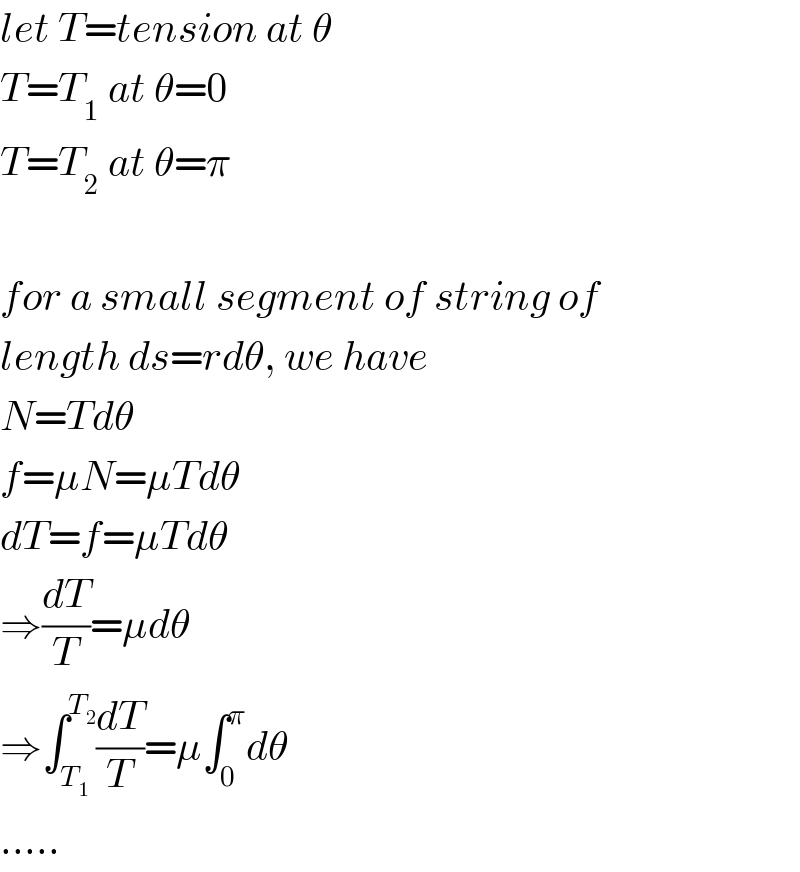
let T=tension at θ T=T_1 at θ=0 T=T_2 at θ=π for a small segment of string of length ds=rdθ, we have N=Tdθ f=μN=μTdθ dT=f=μTdθ ⇒(dT/T)=μdθ ⇒∫_T_1 ^T_2 (dT/T)=μ∫_0 ^π dθ .....
$${let}\:{T}={tension}\:{at}\:\theta \\ $$$${T}={T}_{\mathrm{1}} \:{at}\:\theta=\mathrm{0} \\ $$$${T}={T}_{\mathrm{2}} \:{at}\:\theta=\pi \\ $$$$ \\ $$$${for}\:{a}\:{small}\:{segment}\:{of}\:{string}\:{of} \\ $$$${length}\:{ds}={rd}\theta,\:{we}\:{have} \\ $$$${N}={Td}\theta \\ $$$${f}=\mu{N}=\mu{Td}\theta \\ $$$${dT}={f}=\mu{Td}\theta \\ $$$$\Rightarrow\frac{{dT}}{{T}}=\mu{d}\theta \\ $$$$\Rightarrow\int_{{T}_{\mathrm{1}} } ^{{T}_{\mathrm{2}} } \frac{{dT}}{{T}}=\mu\int_{\mathrm{0}} ^{\pi} {d}\theta \\ $$$$….. \\ $$
Commented by ajfour last updated on 12/Nov/17
it should be 2Tsin ((dθ/2))=dN and df =μdN = −dT ⇒ dT =− μ[2Tsin ((dθ/2))] or dT = −𝛍T d𝛉 with T = T_2 for 𝛉=0 or T = T_1 for 𝛉=𝛑 .
$${it}\:{should}\:{be}\:\mathrm{2}{T}\mathrm{sin}\:\left(\frac{{d}\theta}{\mathrm{2}}\right)={dN} \\ $$$${and}\:\:\:\:\:\:{df}\:=\mu{dN}\:=\:−{dT} \\ $$$$\Rightarrow\:\:\:{dT}\:=−\:\mu\left[\mathrm{2}{T}\mathrm{sin}\:\left(\frac{{d}\theta}{\mathrm{2}}\right)\right] \\ $$$${or}\:\:\:\:\:\:\:\:\boldsymbol{{dT}}\:=\:−\boldsymbol{\mu{T}}\:\boldsymbol{{d}\theta} \\ $$$${with}\:\boldsymbol{{T}}\:=\:\boldsymbol{{T}}_{\mathrm{2}} \:\:{for}\:\boldsymbol{\theta}=\mathrm{0}\:\:{or} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{T}}\:=\:\boldsymbol{{T}}_{\mathrm{1}} \:{for}\:\boldsymbol{\theta}=\boldsymbol{\pi}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *