Question Number 24111 by ajfour last updated on 12/Nov/17
Commented by ajfour last updated on 12/Nov/17

$${Solution}\:{to}\:{Q}.\:\mathrm{24100} \\ $$
Answered by ajfour last updated on 12/Nov/17

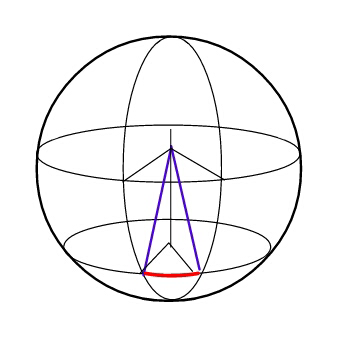
$$\:{let}\:{D}\:{be}\:{distance}\:{between}\:{the} \\ $$$${two}\:{points}\:\left({arc}\:{length}\:{in}\:{red}\right). \\ $$$${Radius}\:{of}\:{latitude}\:\mathrm{65}°{E}\:{be}\:{r}. \\ $$$$\:\:\:\:\boldsymbol{{r}}\:=\:\boldsymbol{{R}}\mathrm{cos}\:\mathrm{65}° \\ $$$$\:\:{D}=\pm\boldsymbol{{r}}\bigtriangleup\boldsymbol{\phi} \\ $$$$\:\:\:\:\:\:=\pm\boldsymbol{{r}}\left({X}°{E}−\mathrm{25}°{E}\right)\frac{\pi}{\mathrm{180}} \\ $$$$\Rightarrow\:\:\:{X}=\mathrm{25}°{E}\pm\frac{\mathrm{180}×\mathrm{7}}{\mathrm{22}}\left(\frac{{D}}{{r}}\right) \\ $$$$\:=\mathrm{25}°{E}\pm\frac{\mathrm{180}×\mathrm{7}}{\mathrm{22}}\left(\frac{\mathrm{2502}.\mathrm{5}{km}}{\mathrm{6370}{km}×\mathrm{cos}\:\mathrm{65}°}\right) \\ $$$$\:\:\:\:\:\:\:{X}=\left(\mathrm{25}\pm\mathrm{53}.\mathrm{24}\right)°{E} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{78}.\mathrm{24}°{E}\:\:{or}\:−\mathrm{28}.\mathrm{24}°{E} \\ $$$$\Rightarrow\:\:\:{X}=\mathrm{78}.\mathrm{24}°{E}\:\:{or}\:\:\mathrm{28}.\mathrm{24}°{W}\:. \\ $$
Commented by tawa tawa last updated on 12/Nov/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}.\: \\ $$
