Question Number 24125 by math solver last updated on 12/Nov/17

Commented by math solver last updated on 12/Nov/17

$$\mathrm{ques}.\mathrm{2}? \\ $$
Answered by ajfour last updated on 12/Nov/17
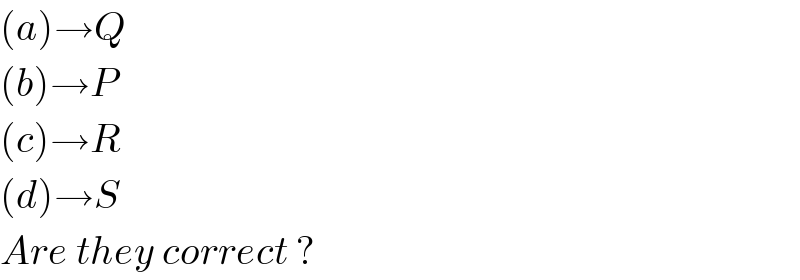
$$\left({a}\right)\rightarrow{Q} \\ $$$$\left({b}\right)\rightarrow{P} \\ $$$$\left({c}\right)\rightarrow{R} \\ $$$$\left({d}\right)\rightarrow{S}\:\:\:\: \\ $$$${Are}\:{they}\:{correct}\:? \\ $$
Commented by ajfour last updated on 13/Nov/17

Commented by math solver last updated on 12/Nov/17
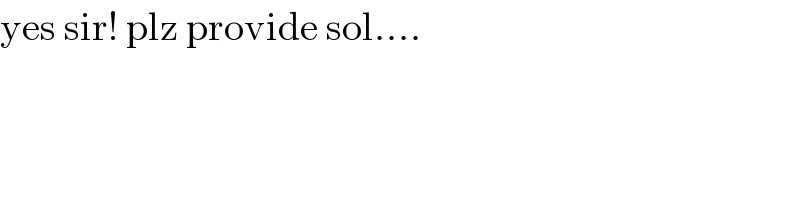
$$\mathrm{yes}\:\mathrm{sir}!\:\mathrm{plz}\:\mathrm{provide}\:\mathrm{sol}…. \\ $$
Commented by ajfour last updated on 13/Nov/17

$${As}\:{time}\:{grows},\:{F}\:{grows}. \\ $$$${First}\:{friction}\:\boldsymbol{{f}}_{\mathrm{2}} \:{rises}\:{in}\:{value} \\ $$$${till}\:{its}\:{maximum}\:\left(=\mu{mg}=\mathrm{2}{N}\right); \\ $$$$\Rightarrow\:\mathrm{20}{t}=\mathrm{2}\:\:\:{or}\:\:\boldsymbol{{t}}=\frac{\mathrm{1}}{\mathrm{10}}\boldsymbol{{s}} \\ $$$$\boldsymbol{{T}}{ension}\:{develops}\:{from}\:{now}, \\ $$$${block}\:{B}\:{starts}\:{accelerating}\:{only} \\ $$$${after}\:\boldsymbol{{f}}_{\mathrm{1}} \:{reaches}\:{its}\:{maximum}. \\ $$$${when}\:\boldsymbol{{f}}_{\mathrm{1}} \:{has}\:{just}\:{reached}\:{its} \\ $$$${maximum},\:{we}\:{have} \\ $$$${Block}\:{A}\:{is}\:{not}\:{started}\:{accelerating}, \\ $$$${so}\:\:\mathrm{2}{T}\:=\:{f}_{\mathrm{1}} =\mathrm{2}{N}\: \\ $$$$\Rightarrow\:\mathrm{3}{T}\:=\mathrm{3}{N}\:\:{and}\:{so} \\ $$$$\:\:\:\:{F}=\mathrm{20}{t}\:−{f}_{\mathrm{2}} −\mathrm{3}{T}\:=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{t}\:=\frac{\mathrm{1}}{\mathrm{4}}\:{s}\:.\:\:{Motion}\:{develops} \\ $$$${from}\:{now}\:{on}\:{and}\:{we}\:{have} \\ $$$$\:\:\:\:\:\mathrm{2}{a}_{{A}} \:=\:\mathrm{3}{a}_{{B}} \\ $$$$\:\:\:\:\mathrm{20}{t}−\mathrm{3}{T}−\mu{mg}\:=\:{ma}_{{B}} \\ $$$$\:\:\:\:\:\mathrm{2}{T}−\mu{mg}\:=\:{ma}_{{A}} \\ $$$$\Rightarrow\:\:\mathrm{40}{t}−\mathrm{5}\mu{mg}\:=\:{m}\left(\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{3}\right){a}_{{A}} \\ $$$${So}\:{at}\:{t}=\mathrm{1}{s} \\ $$$$\:\:\:\:\:{a}_{{A}} =\:\frac{\mathrm{90}}{\mathrm{13}}\:{m}/{s}^{\mathrm{2}} \:. \\ $$
Commented by math solver last updated on 13/Nov/17

$$\mathrm{god}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
