Question Number 24172 by ajfour last updated on 13/Nov/17
Commented by ajfour last updated on 13/Nov/17
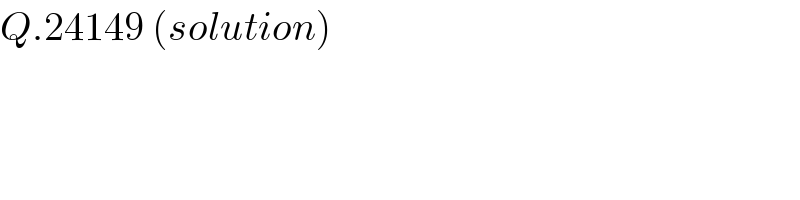
$${Q}.\mathrm{24149}\:\left({solution}\right) \\ $$
Answered by ajfour last updated on 13/Nov/17

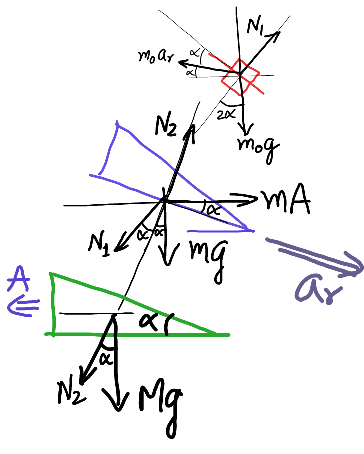
$${Let}\:{acceleration}\:{of}\:{lower}\:{wedge} \\ $$$${be}\:\boldsymbol{{A}},\:{and}\:{relative}\:{acceleration} \\ $$$${of}\:{upper}\:{wedge}\:{with}\:{respect}\:{to} \\ $$$${lower}\:{one}\:{be}\:\boldsymbol{{a}}_{\boldsymbol{{r}}} . \\ $$$${Then}\:{along}\:{normal}\:{to}\:{incline} \\ $$$${of}\:{m},\:{we}\:{have}\:{from}\:{forces}\:{on}\:{m}_{\mathrm{0}} : \\ $$$${m}_{\mathrm{0}} {g}\mathrm{cos}\:\mathrm{2}\alpha+{m}_{\mathrm{0}} {a}_{{r}} \mathrm{sin}\:\alpha\:=\:{N}_{\mathrm{1}} \\ $$$${And}\:{along}\:{normal}\:{to}\:{incline}\:{of} \\ $$$${M},\:{we}\:{have}\:{from}\:{forces}\:{on}\:{m}: \\ $$$${N}_{\mathrm{1}} \mathrm{cos}\:\alpha+{mg}\mathrm{cos}\:\alpha={N}_{\mathrm{2}} +{mA}\mathrm{sin}\:\alpha \\ $$$${Along}\:{incline}\:{of}\:{M},\:{from}\: \\ $$$$\:{forces}\:{on}\:{m}: \\ $$$${mg}\mathrm{sin}\:\alpha+{mA}\mathrm{cos}\:\alpha−{N}_{\mathrm{1}} \mathrm{sin}\:\alpha={ma}_{{r}} \\ $$$${And}\:{along}\:{horizontal},\:{force}\:{on}\: \\ $$$${M}\:{yields}: \\ $$$${N}_{\mathrm{2}} \mathrm{sin}\:\alpha\:=\:{MA} \\ $$$${solving}\:{these}\:,\:{I}\:{arrive}\:{at}\:{result} \\ $$$$\:\:\boldsymbol{{A}}=\frac{\boldsymbol{{m}}\left(\boldsymbol{{m}}+\boldsymbol{{m}}_{\mathrm{0}} \right)\:\boldsymbol{{g}}\mathrm{sin}\:\boldsymbol{\alpha}\mathrm{cos}\:\boldsymbol{\alpha}}{\boldsymbol{{M}}\left(\boldsymbol{{m}}+\boldsymbol{{m}}_{\mathrm{0}} \mathrm{sin}\:^{\mathrm{2}} \boldsymbol{\alpha}\right)+\boldsymbol{{m}}\mathrm{sin}\:^{\mathrm{2}} \boldsymbol{\alpha}\left(\boldsymbol{{m}}−\boldsymbol{{m}}_{\mathrm{0}} \mathrm{cos}\:\mathrm{2}\boldsymbol{\alpha}\right)}\:. \\ $$
