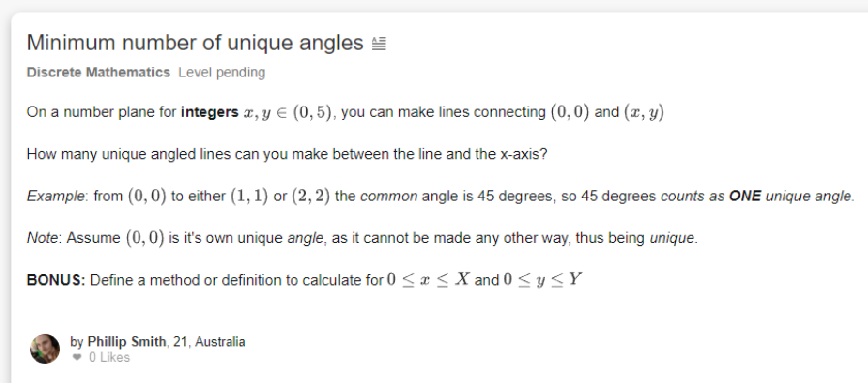
Question Number 24184 by FilupES last updated on 14/Nov/17
Commented by FilupES last updated on 14/Nov/17
$$\mathrm{I}\:\mathrm{will}\:\mathrm{upload}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{my}\:\mathrm{challange}\:\mathrm{later}, \\ $$$$\mathrm{or}\:\mathrm{if}\:\mathrm{requested}! \\ $$
Commented by FilupES last updated on 14/Nov/17
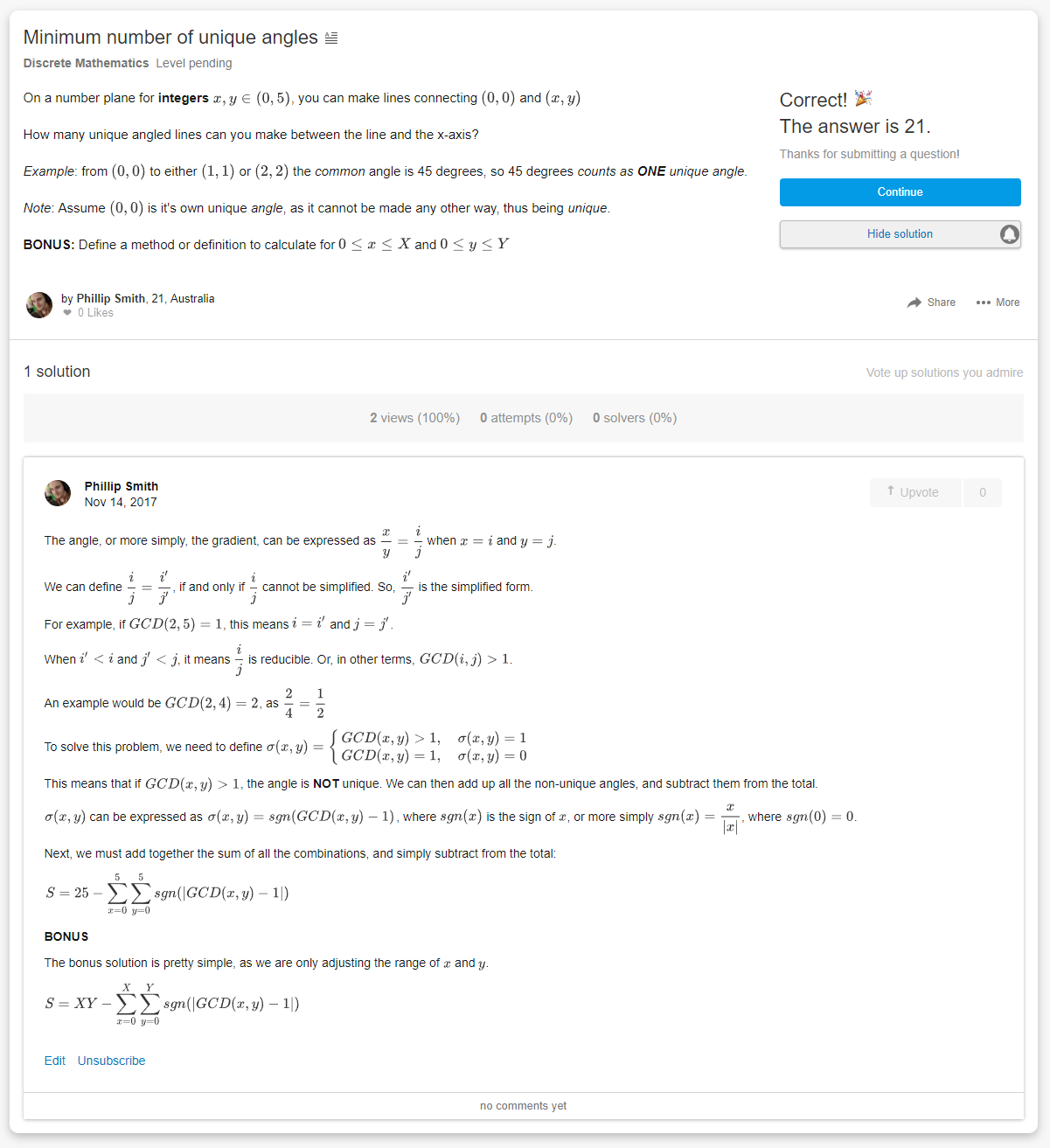
Commented by mrW1 last updated on 14/Nov/17
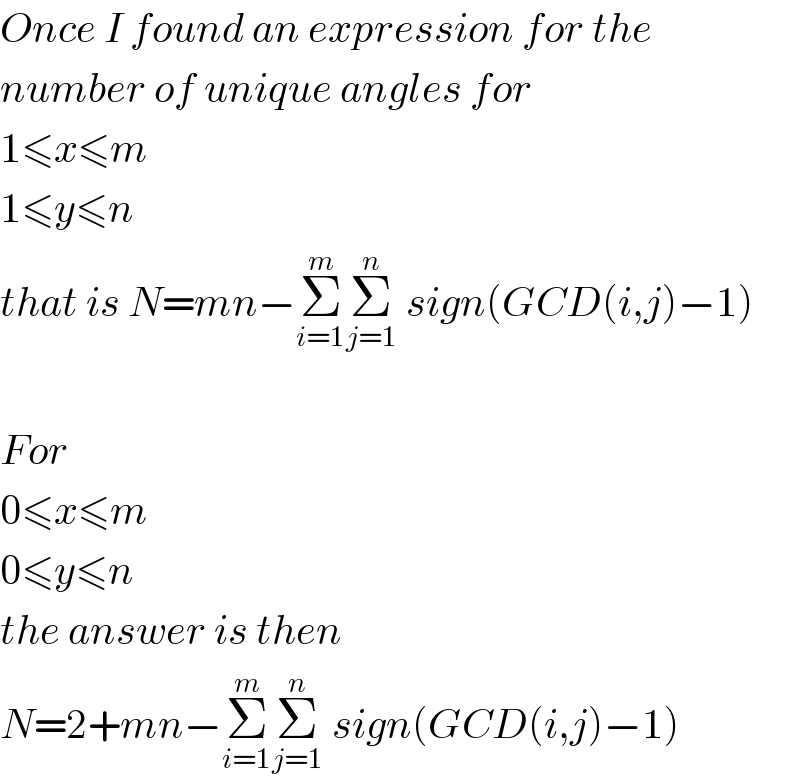
$${Once}\:{I}\:{found}\:{an}\:{expression}\:{for}\:{the} \\ $$$${number}\:{of}\:{unique}\:{angles}\:{for} \\ $$$$\mathrm{1}\leqslant{x}\leqslant{m} \\ $$$$\mathrm{1}\leqslant{y}\leqslant{n} \\ $$$${that}\:{is}\:{N}={mn}−\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\:{sign}\left({GCD}\left({i},{j}\right)−\mathrm{1}\right) \\ $$$$ \\ $$$${For} \\ $$$$\mathrm{0}\leqslant{x}\leqslant{m} \\ $$$$\mathrm{0}\leqslant{y}\leqslant{n} \\ $$$${the}\:{answer}\:{is}\:{then} \\ $$$${N}=\mathrm{2}+{mn}−\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\:{sign}\left({GCD}\left({i},{j}\right)−\mathrm{1}\right) \\ $$
Commented by FilupES last updated on 14/Nov/17

$$\mathrm{why}\:+\mathrm{2}? \\ $$
Commented by mrW1 last updated on 14/Nov/17
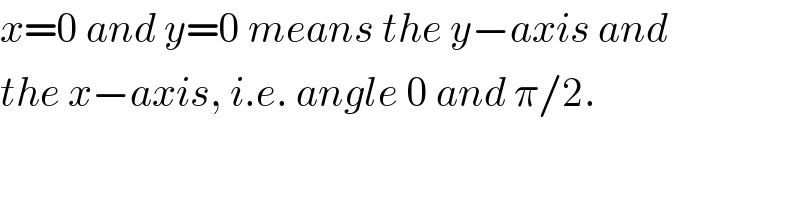
$${x}=\mathrm{0}\:{and}\:{y}=\mathrm{0}\:{means}\:{the}\:{y}−{axis}\:{and} \\ $$$${the}\:{x}−{axis},\:{i}.{e}.\:{angle}\:\mathrm{0}\:{and}\:\pi/\mathrm{2}. \\ $$
Commented by mrW1 last updated on 14/Nov/17

$${I}\:{found}\:{the}\:{original}\:{question}\:#\mathrm{12883}. \\ $$
Commented by FilupES last updated on 14/Nov/17
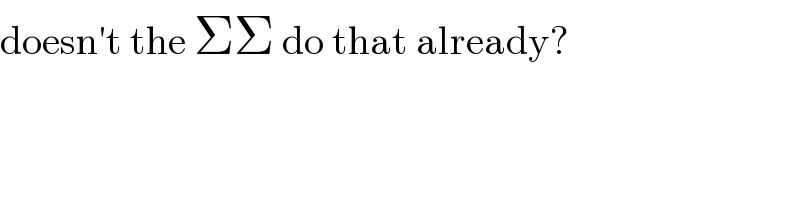
$$\mathrm{doesn}'\mathrm{t}\:\mathrm{the}\:\Sigma\Sigma\:\mathrm{do}\:\mathrm{that}\:\mathrm{already}? \\ $$
Commented by mrW1 last updated on 14/Nov/17
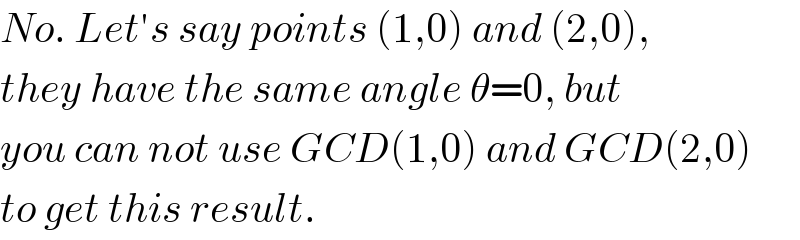
$${No}.\:{Let}'{s}\:{say}\:{points}\:\left(\mathrm{1},\mathrm{0}\right)\:{and}\:\left(\mathrm{2},\mathrm{0}\right), \\ $$$${they}\:{have}\:{the}\:{same}\:{angle}\:\theta=\mathrm{0},\:{but} \\ $$$${you}\:{can}\:{not}\:{use}\:{GCD}\left(\mathrm{1},\mathrm{0}\right)\:{and}\:{GCD}\left(\mathrm{2},\mathrm{0}\right) \\ $$$${to}\:{get}\:{this}\:{result}. \\ $$
Commented by mrW1 last updated on 15/Nov/17
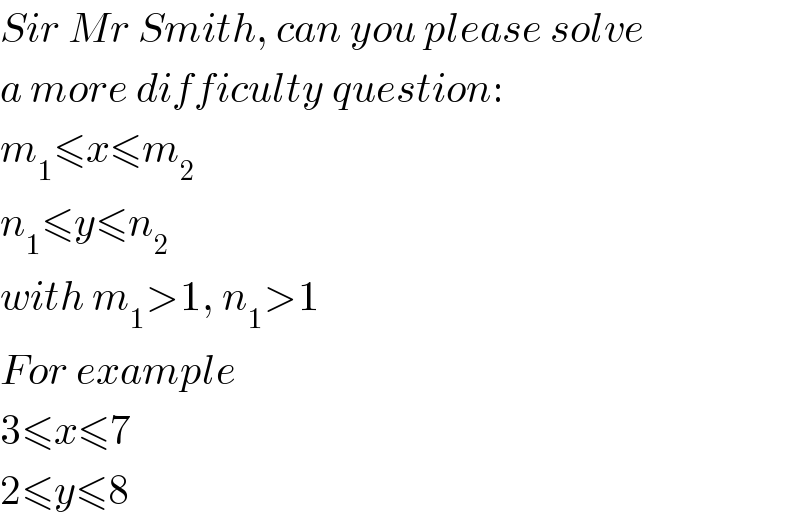
$${Sir}\:{Mr}\:{Smith},\:{can}\:{you}\:{please}\:{solve} \\ $$$${a}\:{more}\:{difficulty}\:{question}: \\ $$$${m}_{\mathrm{1}} \leqslant{x}\leqslant{m}_{\mathrm{2}} \\ $$$${n}_{\mathrm{1}} \leqslant{y}\leqslant{n}_{\mathrm{2}} \\ $$$${with}\:{m}_{\mathrm{1}} >\mathrm{1},\:{n}_{\mathrm{1}} >\mathrm{1} \\ $$$${For}\:{example} \\ $$$$\mathrm{3}\leqslant{x}\leqslant\mathrm{7} \\ $$$$\mathrm{2}\leqslant{y}\leqslant\mathrm{8} \\ $$
