Question Number 24227 by tawa tawa last updated on 14/Nov/17
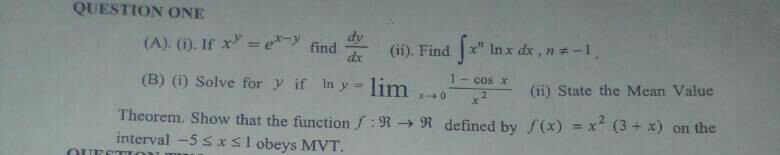
Commented by tawa tawa last updated on 14/Nov/17

$$\mathrm{please}\:\mathrm{help}. \\ $$
Answered by $@ty@m last updated on 14/Nov/17
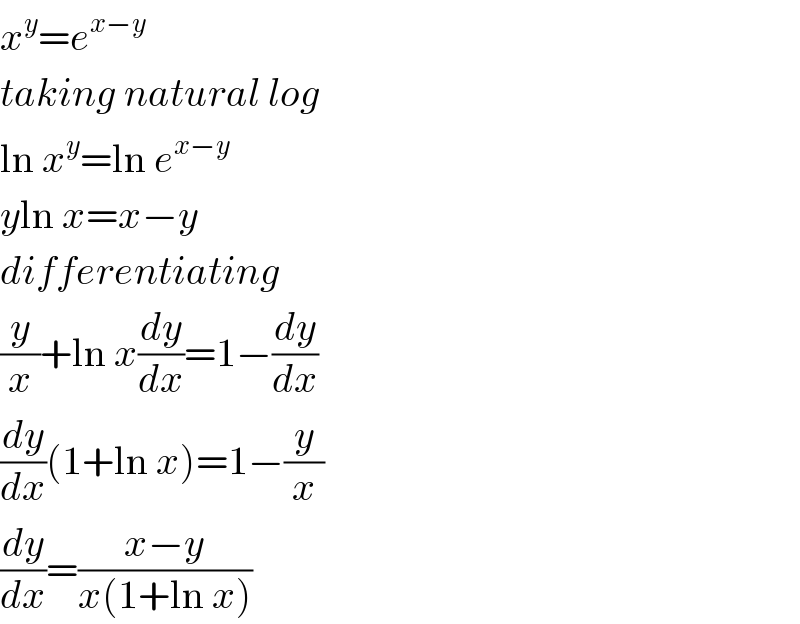
$${x}^{{y}} ={e}^{{x}−{y}} \\ $$$${taking}\:{natural}\:{log} \\ $$$$\mathrm{ln}\:{x}^{{y}} =\mathrm{ln}\:{e}^{{x}−{y}} \\ $$$${y}\mathrm{ln}\:{x}={x}−{y} \\ $$$${differentiating} \\ $$$$\frac{{y}}{{x}}+\mathrm{ln}\:{x}\frac{{dy}}{{dx}}=\mathrm{1}−\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}\left(\mathrm{1}+\mathrm{ln}\:{x}\right)=\mathrm{1}−\frac{{y}}{{x}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{x}−{y}}{{x}\left(\mathrm{1}+\mathrm{ln}\:{x}\right)} \\ $$
Commented by tawa tawa last updated on 16/Nov/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tawa tawa last updated on 14/Nov/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by abwayh last updated on 16/Nov/17
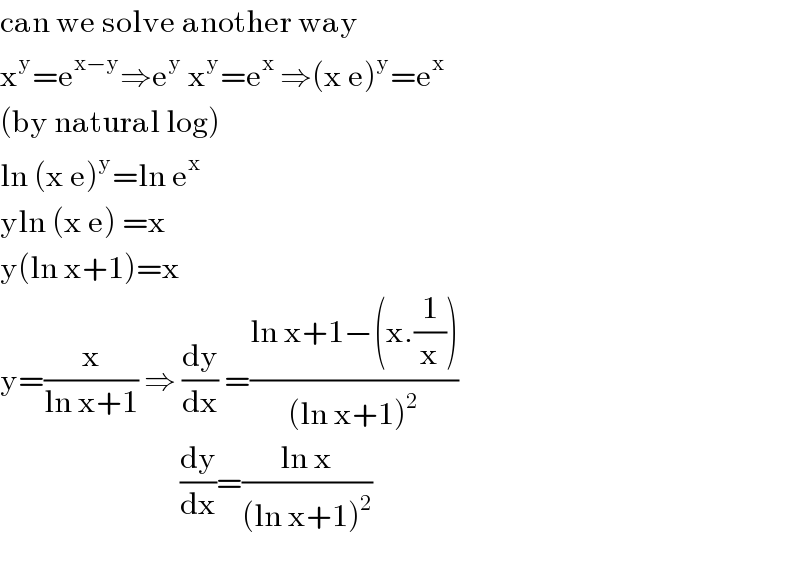
$$\mathrm{can}\:\mathrm{we}\:\mathrm{solve}\:\mathrm{another}\:\mathrm{way} \\ $$$$\mathrm{x}^{\mathrm{y}} =\mathrm{e}^{\mathrm{x}−\mathrm{y}} \Rightarrow\mathrm{e}^{\mathrm{y}} \:\mathrm{x}^{\mathrm{y}} =\mathrm{e}^{\mathrm{x}} \:\Rightarrow\left(\mathrm{x}\:\mathrm{e}\right)^{\mathrm{y}} =\mathrm{e}^{\mathrm{x}} \\ $$$$\left(\mathrm{by}\:\mathrm{natural}\:\mathrm{log}\right) \\ $$$$\mathrm{ln}\:\left(\mathrm{x}\:\mathrm{e}\right)^{\mathrm{y}} =\mathrm{ln}\:\mathrm{e}^{\mathrm{x}} \: \\ $$$$\mathrm{yln}\:\left(\mathrm{x}\:\mathrm{e}\right)\:=\mathrm{x} \\ $$$$\mathrm{y}\left(\mathrm{ln}\:\mathrm{x}+\mathrm{1}\right)=\mathrm{x} \\ $$$$\mathrm{y}=\frac{\mathrm{x}}{\mathrm{ln}\:\mathrm{x}+\mathrm{1}}\:\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\frac{\mathrm{ln}\:\mathrm{x}+\mathrm{1}−\left(\mathrm{x}.\frac{\mathrm{1}}{\mathrm{x}}\right)}{\left(\mathrm{ln}\:\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{ln}\:\mathrm{x}}{\left(\mathrm{ln}\:\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by $@ty@m last updated on 16/Nov/17

$${Its}\:{same} \\ $$
Answered by $@ty@m last updated on 14/Nov/17
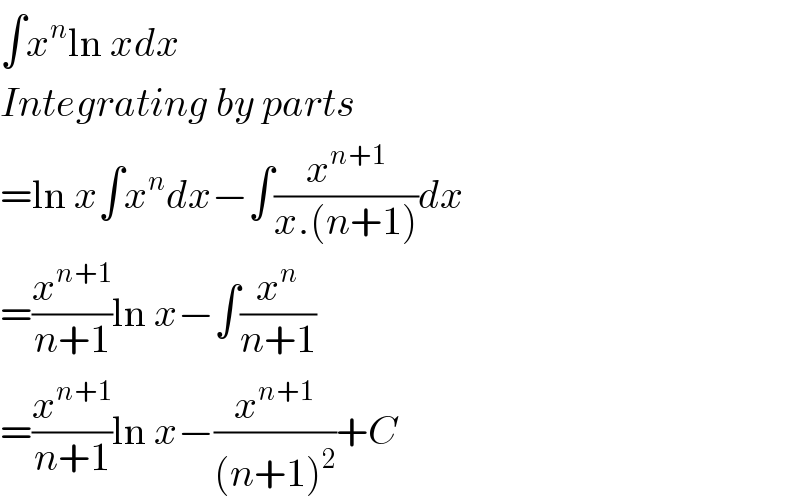
$$\int{x}^{{n}} \mathrm{ln}\:{xdx} \\ $$$${Integrating}\:{by}\:{parts} \\ $$$$=\mathrm{ln}\:{x}\int{x}^{{n}} {dx}−\int\frac{{x}^{{n}+\mathrm{1}} }{{x}.\left({n}+\mathrm{1}\right)}{dx} \\ $$$$=\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mathrm{ln}\:{x}−\int\frac{{x}^{{n}} }{{n}+\mathrm{1}} \\ $$$$=\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mathrm{ln}\:{x}−\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+{C} \\ $$
Commented by tawa tawa last updated on 14/Nov/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by $@ty@m last updated on 14/Nov/17
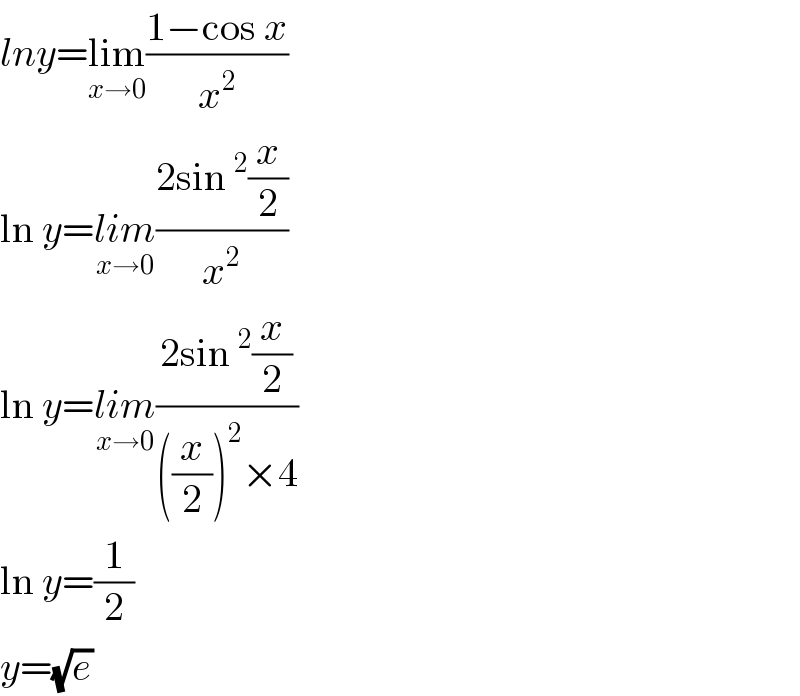
$${lny}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}}{{x}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:{y}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:{y}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} ×\mathrm{4}} \\ $$$$\mathrm{ln}\:{y}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}=\sqrt{{e}} \\ $$
Commented by tawa tawa last updated on 16/Nov/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tawa tawa last updated on 14/Nov/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tawa tawa last updated on 14/Nov/17
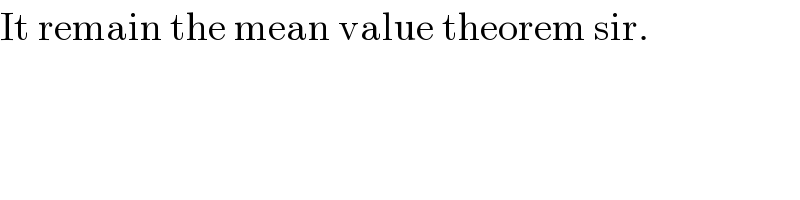
$$\mathrm{It}\:\mathrm{remain}\:\mathrm{the}\:\mathrm{mean}\:\mathrm{value}\:\mathrm{theorem}\:\mathrm{sir}. \\ $$
Commented by abwayh last updated on 16/Nov/17
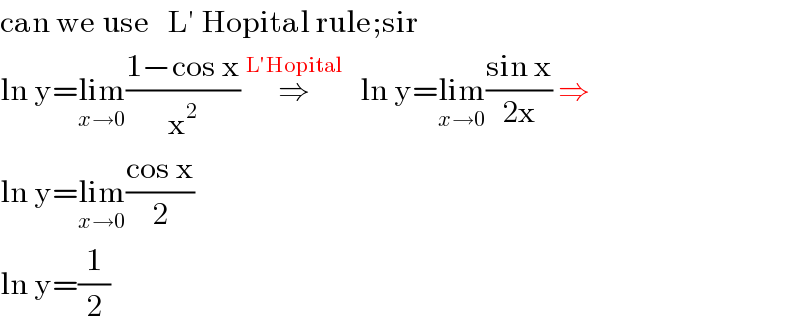
$$\mathrm{can}\:\mathrm{we}\:\mathrm{use}\:\:\:\mathrm{L}'\:\mathrm{Hopital}\:\mathrm{rule};\mathrm{sir} \\ $$$$\mathrm{ln}\:\mathrm{y}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:\overset{\mathrm{L}'\mathrm{Hopital}} {\Rightarrow}\:\:\:\mathrm{ln}\:\mathrm{y}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{2x}}\:\Rightarrow \\ $$$$\mathrm{ln}\:\mathrm{y}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{2}} \\ $$$$\mathrm{ln}\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by $@ty@m last updated on 16/Nov/17
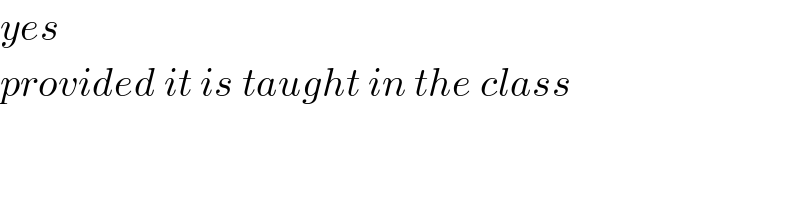
$${yes} \\ $$$${provided}\:{it}\:{is}\:{taught}\:{in}\:{the}\:{class} \\ $$
