Question Number 24524 by mondodotto@gmail.com last updated on 20/Nov/17
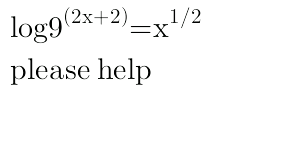
Answered by mrW1 last updated on 20/Nov/17
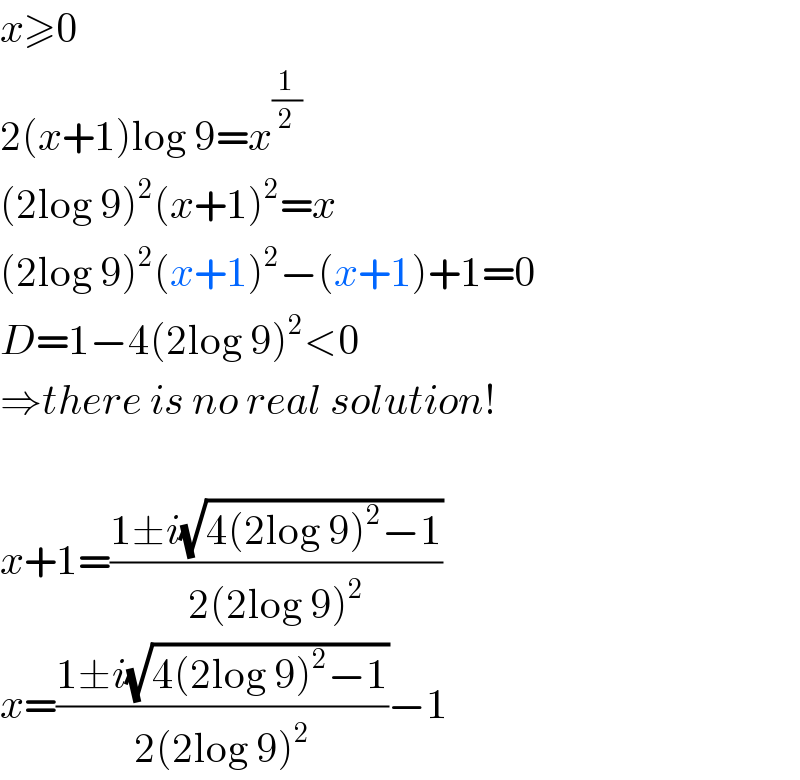
$${x}\geqslant\mathrm{0} \\ $$$$\mathrm{2}\left({x}+\mathrm{1}\right)\mathrm{log}\:\mathrm{9}={x}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\left(\mathrm{2log}\:\mathrm{9}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} ={x} \\ $$$$\left(\mathrm{2log}\:\mathrm{9}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} −\left({x}+\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$${D}=\mathrm{1}−\mathrm{4}\left(\mathrm{2log}\:\mathrm{9}\right)^{\mathrm{2}} <\mathrm{0} \\ $$$$\Rightarrow{there}\:{is}\:{no}\:{real}\:{solution}! \\ $$$$ \\ $$$${x}+\mathrm{1}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{4}\left(\mathrm{2log}\:\mathrm{9}\right)^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}\left(\mathrm{2log}\:\mathrm{9}\right)^{\mathrm{2}} } \\ $$$${x}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{4}\left(\mathrm{2log}\:\mathrm{9}\right)^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}\left(\mathrm{2log}\:\mathrm{9}\right)^{\mathrm{2}} }−\mathrm{1} \\ $$
Commented by Rasheed.Sindhi last updated on 20/Nov/17

$$\mathcal{V}.\:\mathcal{N}{ice}\:\mathcal{S}{ir}! \\ $$
