Question Number 24704 by math solver last updated on 25/Nov/17

Commented by math solver last updated on 25/Nov/17
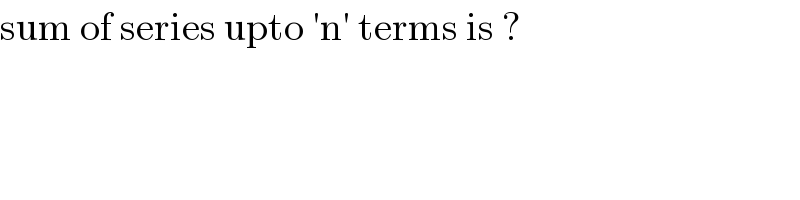
$$\mathrm{sum}\:\mathrm{of}\:\mathrm{series}\:\mathrm{upto}\:'\mathrm{n}'\:\mathrm{terms}\:\mathrm{is}\:? \\ $$
Commented by prakash jain last updated on 25/Nov/17
![T_i =(.5)^3 ×(i+1)^3 S_n =Σ_(i=1) ^n (.5)^3 ×(i+1)^3 =(.5)^3 [Σ_(i=0) ^(n+1) i^3 −1] =(.5)^3 [{(((n+1)(n+2))/2)}^2 −1]](https://www.tinkutara.com/question/Q24708.png)
$${T}_{{i}} =\left(.\mathrm{5}\right)^{\mathrm{3}} ×\left({i}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$${S}_{{n}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(.\mathrm{5}\right)^{\mathrm{3}} ×\left({i}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$=\left(.\mathrm{5}\right)^{\mathrm{3}} \left[\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}{i}^{\mathrm{3}} −\mathrm{1}\right] \\ $$$$=\left(.\mathrm{5}\right)^{\mathrm{3}} \left[\left\{\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{2}}\right\}^{\mathrm{2}} −\mathrm{1}\right] \\ $$
Commented by math solver last updated on 25/Nov/17

$$\mathrm{gracias}. \\ $$
Commented by math solver last updated on 25/Nov/17
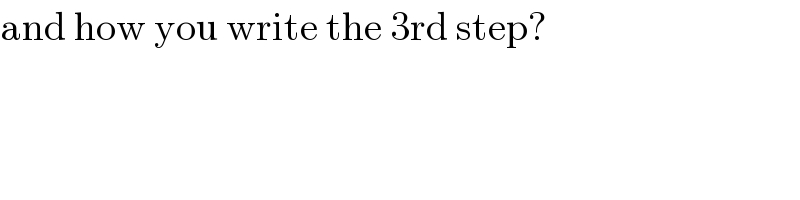
$$\mathrm{and}\:\mathrm{how}\:\mathrm{you}\:\mathrm{write}\:\mathrm{the}\:\mathrm{3rd}\:\mathrm{step}? \\ $$
Commented by jota+ last updated on 25/Nov/17
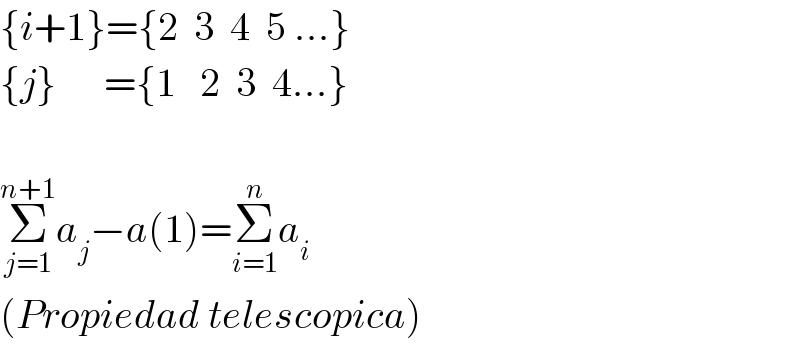
$$\left\{{i}+\mathrm{1}\right\}=\left\{\mathrm{2}\:\:\mathrm{3}\:\:\mathrm{4}\:\:\mathrm{5}\:…\right\} \\ $$$$\left\{{j}\right\}\:\:\:\:\:\:=\left\{\mathrm{1}\:\:\:\mathrm{2}\:\:\mathrm{3}\:\:\mathrm{4}…\right\} \\ $$$$ \\ $$$$\underset{{j}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{a}_{{j}} −{a}\left(\mathrm{1}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} \\ $$$$\left({Propiedad}\:{telescopica}\right) \\ $$
Answered by jota+ last updated on 25/Nov/17
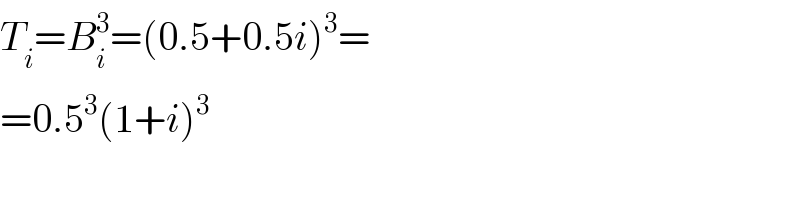
$${T}_{{i}} ={B}_{{i}} ^{\mathrm{3}} =\left(\mathrm{0}.\mathrm{5}+\mathrm{0}.\mathrm{5}{i}\right)^{\mathrm{3}} = \\ $$$$=\mathrm{0}.\mathrm{5}^{\mathrm{3}} \left(\mathrm{1}+{i}\right)^{\mathrm{3}} \\ $$
