Question Number 24712 by ajfour last updated on 25/Nov/17

Commented by ajfour last updated on 25/Nov/17

$${Originally}\:{a}\:{planet}\:{of}\:{radius}\:\boldsymbol{{R}}, \\ $$$${of}\:{uniform}\:{density},\:{has}\:{a}\:{gravitational} \\ $$$${field}\:{at}\:{its}\:{surface}\:{equal}\:{to}\:\:\boldsymbol{{g}}. \\ $$$${Because}\:{a}\:{sphere}\:{of}\:{crust}\:{of} \\ $$$${radius}\:\boldsymbol{{r}}\:{is}\:{removed}\:{gravitational} \\ $$$${field}\:{experienced}\:{by}\:{the}\:{figure} \\ $$$${at}\:{the}\:{surface}\:{reduces}\:{to}\:\boldsymbol{{g}}/\mathrm{2}. \\ $$$${Find}\:\boldsymbol{{r}}/\boldsymbol{{R}}\:.\: \\ $$
Commented by mrW1 last updated on 25/Nov/17
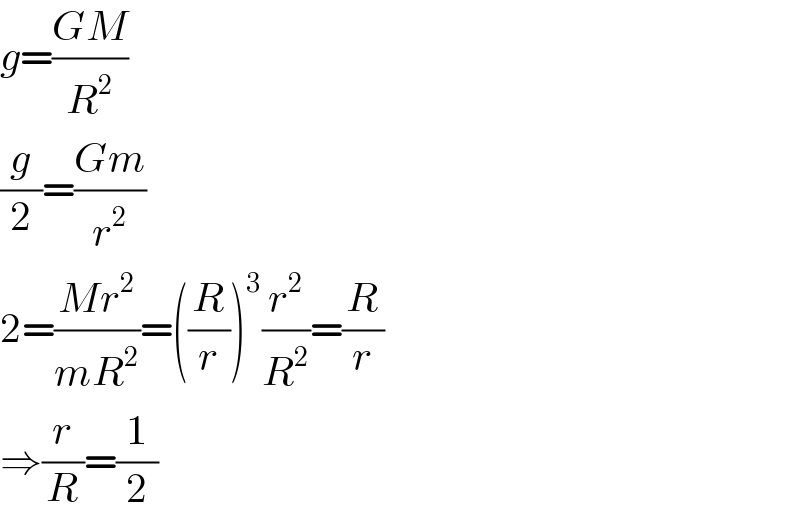
$${g}=\frac{{GM}}{{R}^{\mathrm{2}} } \\ $$$$\frac{{g}}{\mathrm{2}}=\frac{{Gm}}{{r}^{\mathrm{2}} } \\ $$$$\mathrm{2}=\frac{{Mr}^{\mathrm{2}} }{{mR}^{\mathrm{2}} }=\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} \frac{{r}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\frac{{R}}{{r}} \\ $$$$\Rightarrow\frac{{r}}{{R}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 25/Nov/17

$${thank}\:{you}\:{Sir}. \\ $$
