Question Number 24877 by Tinkutara last updated on 28/Nov/17

Commented by Tinkutara last updated on 28/Nov/17
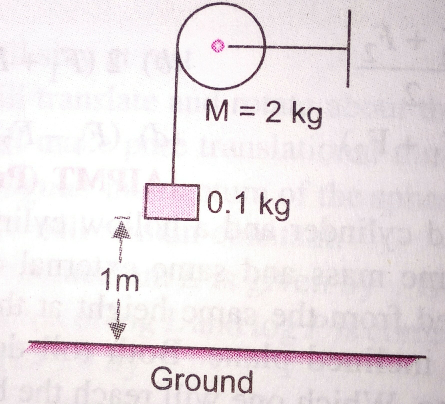
Commented by mrW1 last updated on 29/Nov/17
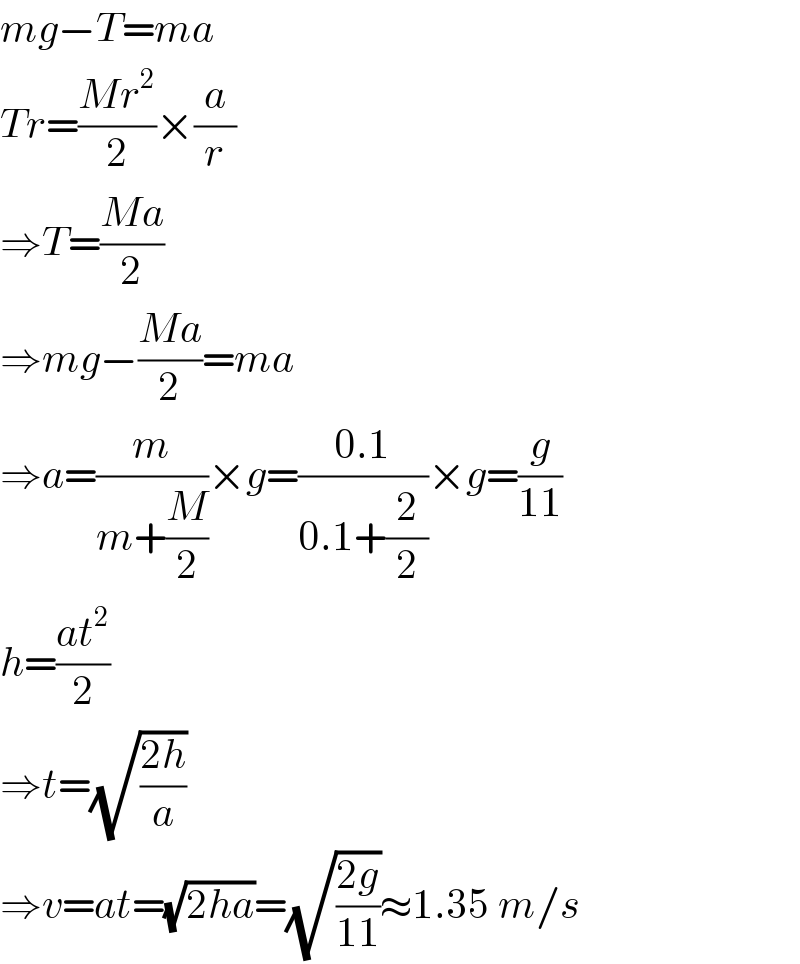
$${mg}−{T}={ma} \\ $$$${Tr}=\frac{{Mr}^{\mathrm{2}} }{\mathrm{2}}×\frac{{a}}{{r}} \\ $$$$\Rightarrow{T}=\frac{{Ma}}{\mathrm{2}} \\ $$$$\Rightarrow{mg}−\frac{{Ma}}{\mathrm{2}}={ma} \\ $$$$\Rightarrow{a}=\frac{{m}}{{m}+\frac{{M}}{\mathrm{2}}}×{g}=\frac{\mathrm{0}.\mathrm{1}}{\mathrm{0}.\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}}}×{g}=\frac{{g}}{\mathrm{11}} \\ $$$${h}=\frac{{at}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow{t}=\sqrt{\frac{\mathrm{2}{h}}{{a}}} \\ $$$$\Rightarrow{v}={at}=\sqrt{\mathrm{2}{ha}}=\sqrt{\frac{\mathrm{2}{g}}{\mathrm{11}}}\approx\mathrm{1}.\mathrm{35}\:{m}/{s} \\ $$
Commented by ajfour last updated on 28/Nov/17

$${please}\:{explain}. \\ $$
Commented by ajfour last updated on 28/Nov/17

$${If}\:{the}\:{string}\:{is}\:{simply}\:{wrapped} \\ $$$${and}\:{pulley}\:{frictionless},\:{then} \\ $$$${mass}\:{falls}\:{freely}. \\ $$$${v}^{\mathrm{2}} =\mathrm{2}{gh}\:=\mathrm{2}\left(\mathrm{9}.\mathrm{8}{m}/{s}^{\mathrm{2}} \right)\left(\mathrm{1}{m}\right) \\ $$$${v}=\sqrt{\mathrm{19}.\mathrm{6}}\:{m}/{s}\:. \\ $$
Commented by Tinkutara last updated on 29/Nov/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}! \\ $$
Commented by jota+ last updated on 28/Nov/17
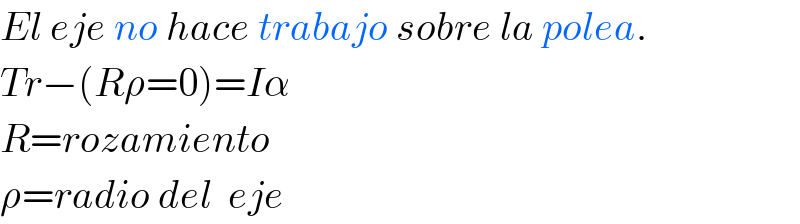
$${El}\:{eje}\:{no}\:{hace}\:{trabajo}\:{sobre}\:{la}\:{polea}. \\ $$$${Tr}−\left({R}\rho=\mathrm{0}\right)={I}\alpha \\ $$$${R}={rozamiento} \\ $$$$\rho={radio}\:{del}\:\:{eje} \\ $$
Commented by mrW1 last updated on 29/Nov/17
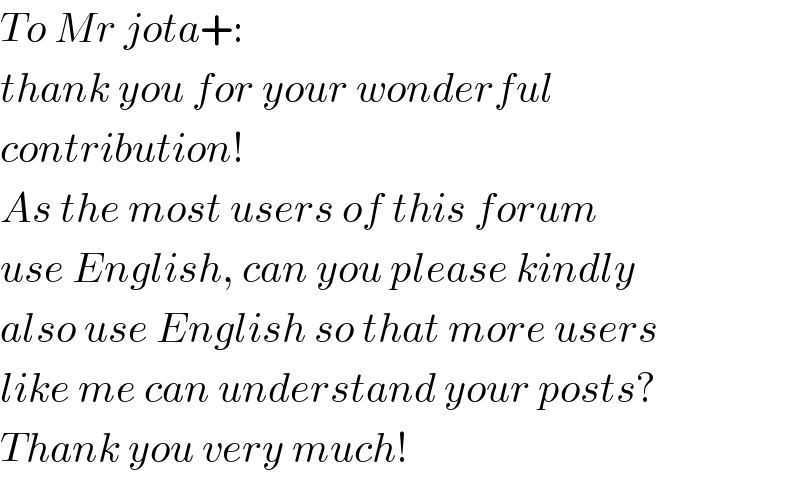
$${To}\:{Mr}\:{jota}+:\: \\ $$$${thank}\:{you}\:{for}\:{your}\:{wonderful}\: \\ $$$${contribution}! \\ $$$${As}\:{the}\:{most}\:{users}\:{of}\:{this}\:{forum} \\ $$$${use}\:{English},\:{can}\:{you}\:{please}\:{kindly} \\ $$$${also}\:{use}\:{English}\:{so}\:{that}\:{more}\:{users} \\ $$$${like}\:{me}\:{can}\:{understand}\:{your}\:{posts}?\: \\ $$$${Thank}\:{you}\:{very}\:{much}! \\ $$
