Question Number 24937 by kosarrr last updated on 29/Nov/17

Commented by behi.8.3.4.17@gmail.com last updated on 29/Nov/17
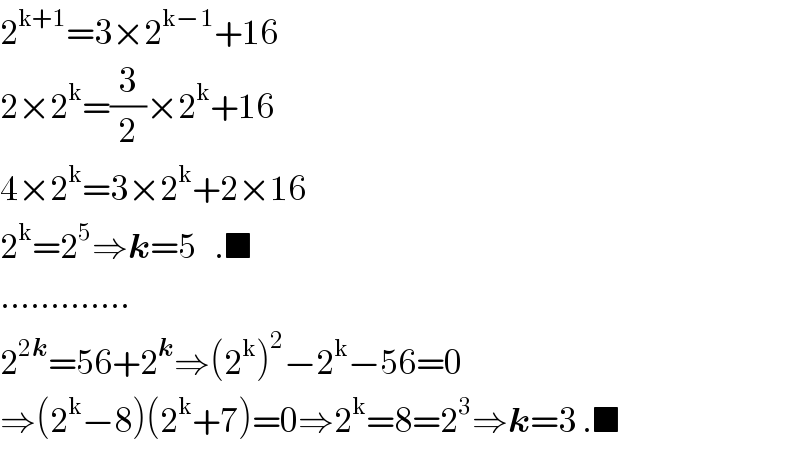
$$\mathrm{2}^{\mathrm{k}+\mathrm{1}} =\mathrm{3}×\mathrm{2}^{\mathrm{k}−\mathrm{1}} +\mathrm{16} \\ $$$$\mathrm{2}×\mathrm{2}^{\mathrm{k}} =\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{2}^{\mathrm{k}} +\mathrm{16} \\ $$$$\mathrm{4}×\mathrm{2}^{\mathrm{k}} =\mathrm{3}×\mathrm{2}^{\mathrm{k}} +\mathrm{2}×\mathrm{16} \\ $$$$\mathrm{2}^{\mathrm{k}} =\mathrm{2}^{\mathrm{5}} \Rightarrow\boldsymbol{{k}}=\mathrm{5}\:\:\:.\blacksquare \\ $$$$…………. \\ $$$$\mathrm{2}^{\mathrm{2}\boldsymbol{{k}}} =\mathrm{56}+\mathrm{2}^{\boldsymbol{{k}}} \Rightarrow\left(\mathrm{2}^{\mathrm{k}} \right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{k}} −\mathrm{56}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}^{\mathrm{k}} −\mathrm{8}\right)\left(\mathrm{2}^{\mathrm{k}} +\mathrm{7}\right)=\mathrm{0}\Rightarrow\mathrm{2}^{\mathrm{k}} =\mathrm{8}=\mathrm{2}^{\mathrm{3}} \Rightarrow\boldsymbol{{k}}=\mathrm{3}\:.\blacksquare \\ $$
