Menu Close

Question-24981

Tinku Tara 0 Comments
Pin




Question Number 24981 by tawa tawa last updated on 30/Nov/17
Commented by tawa tawa last updated on 30/Nov/17
please help.
$$\mathrm{please}\:\mathrm{help}. \\ $$
Answered by kaivan.ahmadi last updated on 13/Dec/17
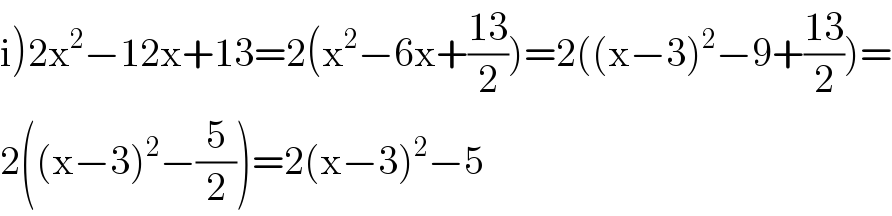
i)2x^2 −12x+13=2(x^2 −6x+((13)/2))=2((x−3)^2 −9+((13)/2))= 2((x−3)^2 −(5/2))=2(x−3)^2 −5
$$\left.\mathrm{i}\right)\mathrm{2x}^{\mathrm{2}} −\mathrm{12x}+\mathrm{13}=\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\frac{\mathrm{13}}{\mathrm{2}}\right)=\mathrm{2}\left(\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{9}+\frac{\mathrm{13}}{\mathrm{2}}\right)= \\ $$$$\mathrm{2}\left(\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}\right)=\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{5} \\ $$
Answered by kaivan.ahmadi last updated on 13/Dec/17
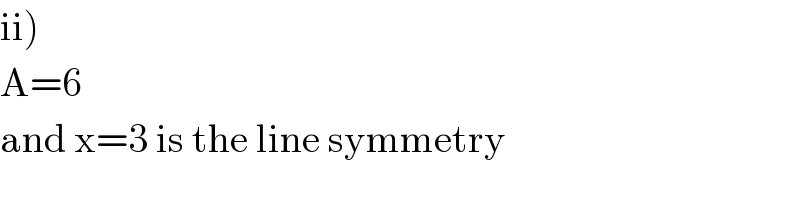
ii) A=6 and x=3 is the line symmetry
$$\left.\mathrm{ii}\right) \\ $$$$\mathrm{A}=\mathrm{6} \\ $$$$\mathrm{and}\:\mathrm{x}=\mathrm{3}\:\mathrm{is}\:\mathrm{the}\:\mathrm{line}\:\mathrm{symmetry} \\ $$
Answered by kaivan.ahmadi last updated on 13/Dec/17
iii)if o≤x≤6 then Min(y)=2(3−3)^2 −5=−5 Max(y)=2(0−3)^2 −5=13 R_f =[−5, 13]
$$\left.\mathrm{iii}\right)\mathrm{if}\:\mathrm{o}\leqslant\mathrm{x}\leqslant\mathrm{6}\:\mathrm{then} \\ $$$$\mathrm{Min}\left(\mathrm{y}\right)=\mathrm{2}\left(\mathrm{3}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{5}=−\mathrm{5} \\ $$$$\mathrm{Max}\left(\mathrm{y}\right)=\mathrm{2}\left(\mathrm{0}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{5}=\mathrm{13} \\ $$$$\mathrm{R}_{\mathrm{f}} =\left[−\mathrm{5},\:\mathrm{13}\right] \\ $$
Answered by kaivan.ahmadi last updated on 13/Dec/17
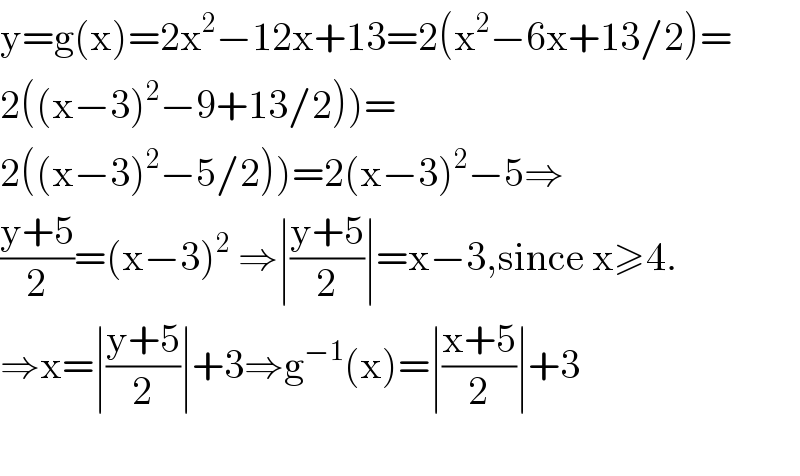
y=g(x)=2x^2 −12x+13=2(x^2 −6x+13/2)= 2((x−3)^2 −9+13/2))= 2((x−3)^2 −5/2))=2(x−3)^2 −5⇒ ((y+5)/2)=(x−3)^2 ⇒∣((y+5)/2)∣=x−3,since x≥4. ⇒x=∣((y+5)/2)∣+3⇒g^(−1) (x)=∣((x+5)/2)∣+3
$$\mathrm{y}=\mathrm{g}\left(\mathrm{x}\right)=\mathrm{2x}^{\mathrm{2}} −\mathrm{12x}+\mathrm{13}=\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{13}/\mathrm{2}\right)= \\ $$$$\left.\mathrm{2}\left(\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{9}+\mathrm{13}/\mathrm{2}\right)\right)= \\ $$$$\left.\mathrm{2}\left(\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{5}/\mathrm{2}\right)\right)=\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{5}\Rightarrow \\ $$$$\frac{\mathrm{y}+\mathrm{5}}{\mathrm{2}}=\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} \:\Rightarrow\mid\frac{\mathrm{y}+\mathrm{5}}{\mathrm{2}}\mid=\mathrm{x}−\mathrm{3},\mathrm{since}\:\mathrm{x}\geqslant\mathrm{4}. \\ $$$$\Rightarrow\mathrm{x}=\mid\frac{\mathrm{y}+\mathrm{5}}{\mathrm{2}}\mid+\mathrm{3}\Rightarrow\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right)=\mid\frac{\mathrm{x}+\mathrm{5}}{\mathrm{2}}\mid+\mathrm{3} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *