Question Number 25074 by Mr easy last updated on 03/Dec/17
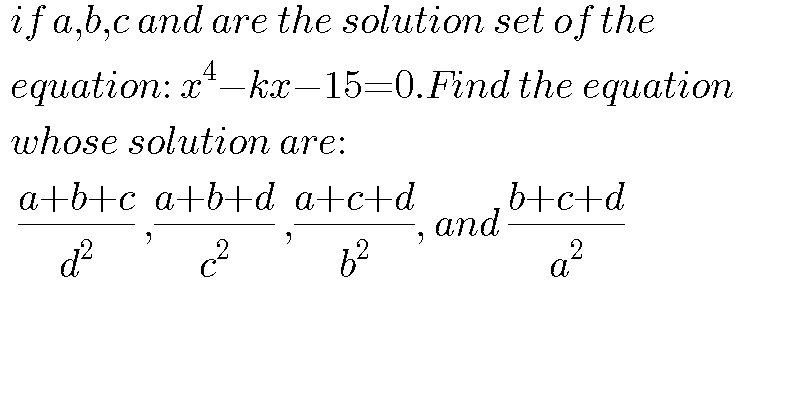
Commented by moxhix last updated on 03/Dec/17

$$\left({x}−{a}\right)\left({x}−{b}\right)\left({x}−{c}\right)\left({x}−{d}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} −\left({a}+{b}+{c}+{d}\right){x}^{\mathrm{3}} +\left({ab}+{bc}+{cd}+{da}\right){x}^{\mathrm{2}} −\left({abc}+{bcd}+{cda}+{dab}\right){x}+{abcd}=\mathrm{0} \\ $$$$\begin{cases}{{a}+{b}+{c}+{d}=\mathrm{0}}\\{{ab}+{bc}+{cd}+{da}=\mathrm{0}}\\{{abc}+{bcd}+{cda}+{dab}={k}}\\{{abcd}=−\mathrm{15}}\end{cases} \\ $$$$\frac{{a}+{b}+{c}}{{d}^{\mathrm{2}} }=\frac{{a}+{b}+{c}+{d}}{{d}^{\mathrm{2}} }−\frac{\mathrm{1}}{{d}}=−\frac{\mathrm{1}}{{d}} \\ $$$${so} \\ $$$$\left({x}−\frac{{a}+{b}+{c}}{{d}^{\mathrm{2}} }\right)\left({x}−\frac{{b}+{c}+{d}}{{a}^{\mathrm{2}} }\right)\left({x}−\frac{{c}+{d}+{a}}{{b}^{\mathrm{2}} }\right)\left({x}−\frac{{d}+{a}+{b}}{{c}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{d}}\right)\left({x}+\frac{\mathrm{1}}{{a}}\right)\left({x}+\frac{\mathrm{1}}{{b}}\right)\left({x}+\frac{\mathrm{1}}{{c}}\right)=\mathrm{0}\:\:\:\:\:\:\left(\downarrow×{abcd}\neq\mathrm{0}\right) \\ $$$$\left({ax}+\mathrm{1}\right)\left({bx}+\mathrm{1}\right)\left({cx}+\mathrm{1}\right)\left({dx}+\mathrm{1}\right)=\mathrm{0} \\ $$$${abcdx}^{\mathrm{4}} +\left({abc}+{bcd}+{cda}+{dab}\right){x}^{\mathrm{3}} +\left({ab}+{bc}+{cd}+{da}\right){x}^{\mathrm{2}} +\left({a}+{b}+{c}+{d}\right){x}+\mathrm{1}=\mathrm{0} \\ $$$$−\mathrm{15}{x}^{\mathrm{4}} +{kx}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{15}{x}^{\mathrm{4}} −{kx}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$$$\therefore{A}\left(\mathrm{15}{x}^{\mathrm{4}} −{kx}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{0}\:\:\left({A}\neq\mathrm{0}\right) \\ $$
