Question Number 25086 by Tinkutara last updated on 03/Dec/17

Commented by Tinkutara last updated on 03/Dec/17
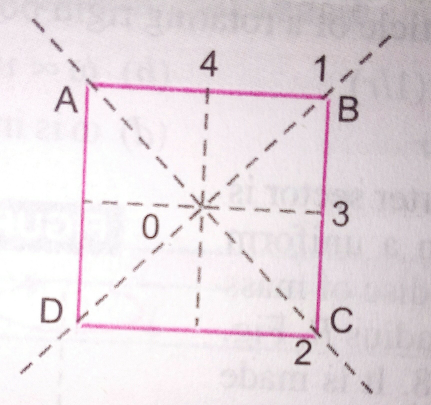
Commented by ajfour last updated on 04/Dec/17

$${I}_{{z}} ={I}_{\mathrm{1}} +{I}_{\mathrm{2}} ={I}_{\mathrm{3}} +{I}_{\mathrm{4}} \:\:\:\:\left(\bot\:{axes}\:{theorem}\right) \\ $$$${where}\:{axes}\:{if}\:{z}\:{is}\:{through}\:{O}\:{and} \\ $$$${perpendicular}\:{to}\:{plane}\:{of}\:{plate}. \\ $$$${for}\:{a}\:{square}\:{plate}\:{I}_{\mathrm{1}} ={I}_{\mathrm{2}} ={I}_{\mathrm{3}} ={I}_{\mathrm{4}} \:. \\ $$$${so}\:{even}\:\left({c}\right)\:{is}\:{true}. \\ $$
Commented by Tinkutara last updated on 03/Dec/17

$${But}\:{answer}\:{is}\:{given}\:\left({c}\right)\:{option}\:{also}. \\ $$
Commented by Tinkutara last updated on 05/Dec/17

$${Why}\:{I}_{\mathrm{1}} ={I}_{\mathrm{3}} ? \\ $$
