Question Number 25094 by ifcrna380w last updated on 03/Dec/17

Answered by mrW1 last updated on 04/Dec/17
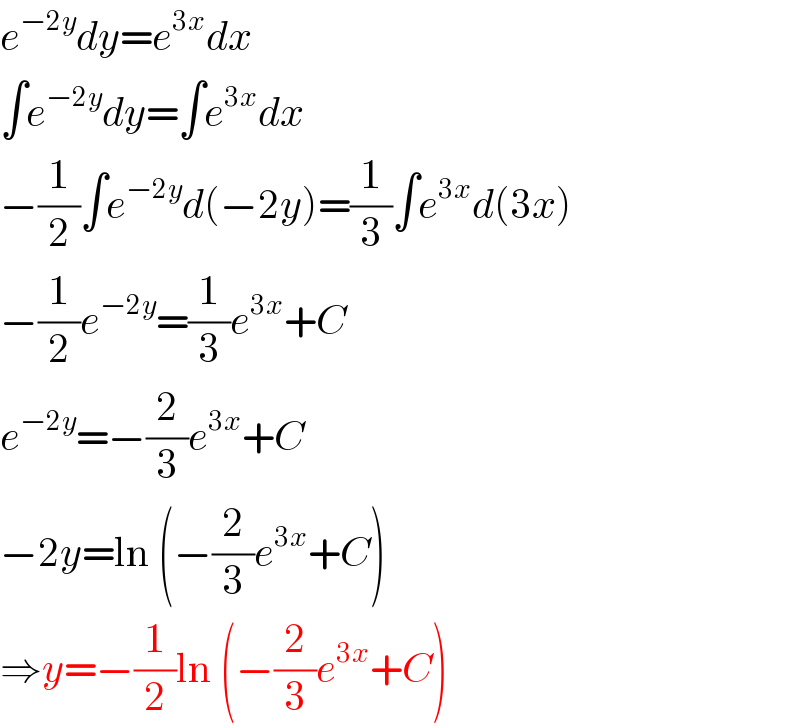
$${e}^{−\mathrm{2}{y}} {dy}={e}^{\mathrm{3}{x}} {dx} \\ $$$$\int{e}^{−\mathrm{2}{y}} {dy}=\int{e}^{\mathrm{3}{x}} {dx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int{e}^{−\mathrm{2}{y}} {d}\left(−\mathrm{2}{y}\right)=\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{\mathrm{3}{x}} {d}\left(\mathrm{3}{x}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}{y}} =\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} +{C} \\ $$$${e}^{−\mathrm{2}{y}} =−\frac{\mathrm{2}}{\mathrm{3}}{e}^{\mathrm{3}{x}} +{C} \\ $$$$−\mathrm{2}{y}=\mathrm{ln}\:\left(−\frac{\mathrm{2}}{\mathrm{3}}{e}^{\mathrm{3}{x}} +{C}\right) \\ $$$$\Rightarrow{y}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(−\frac{\mathrm{2}}{\mathrm{3}}{e}^{\mathrm{3}{x}} +{C}\right) \\ $$
