Question Number 25129 by mondodotto@gmail.com last updated on 04/Dec/17
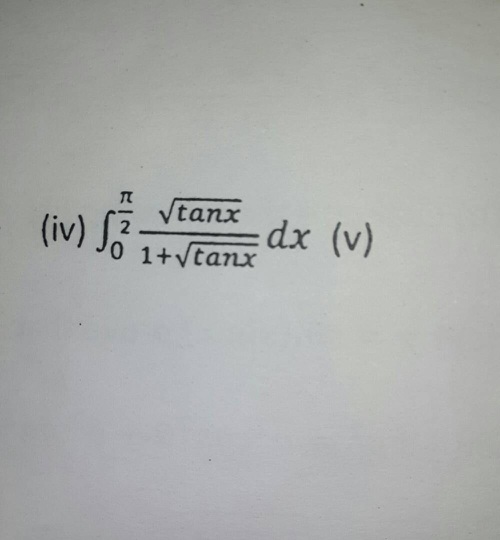
Commented by mondodotto@gmail.com last updated on 04/Dec/17
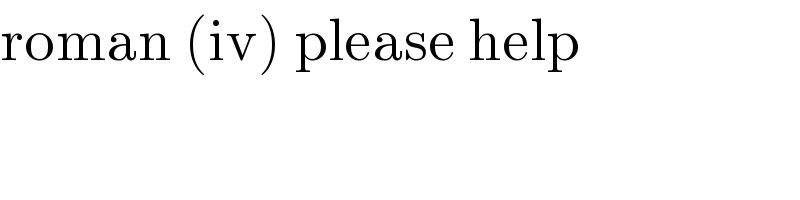
$$\mathrm{roman}\:\left(\mathrm{iv}\right)\:\mathrm{please}\:\mathrm{help} \\ $$
Answered by ajfour last updated on 05/Dec/17
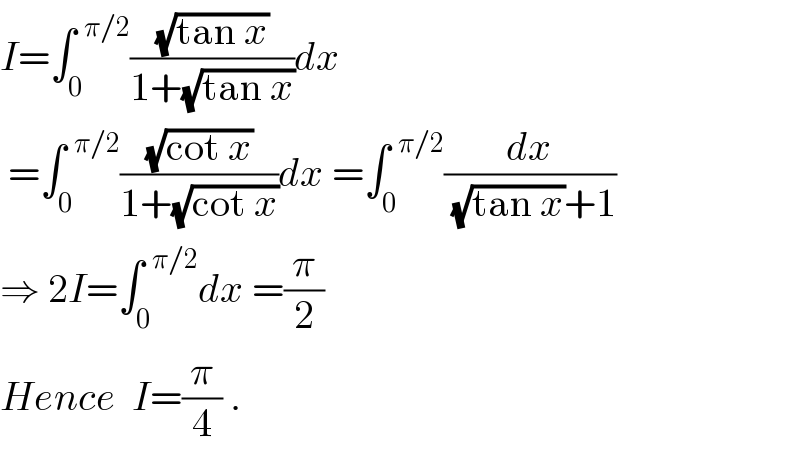
$${I}=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}}{dx} \\ $$$$\:=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \frac{\sqrt{\mathrm{cot}\:{x}}}{\mathrm{1}+\sqrt{\mathrm{cot}\:{x}}}{dx}\:=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \frac{{dx}}{\:\sqrt{\mathrm{tan}\:{x}}+\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} {dx}\:=\frac{\pi}{\mathrm{2}} \\ $$$${Hence}\:\:{I}=\frac{\pi}{\mathrm{4}}\:. \\ $$
Commented by prakash jain last updated on 05/Dec/17
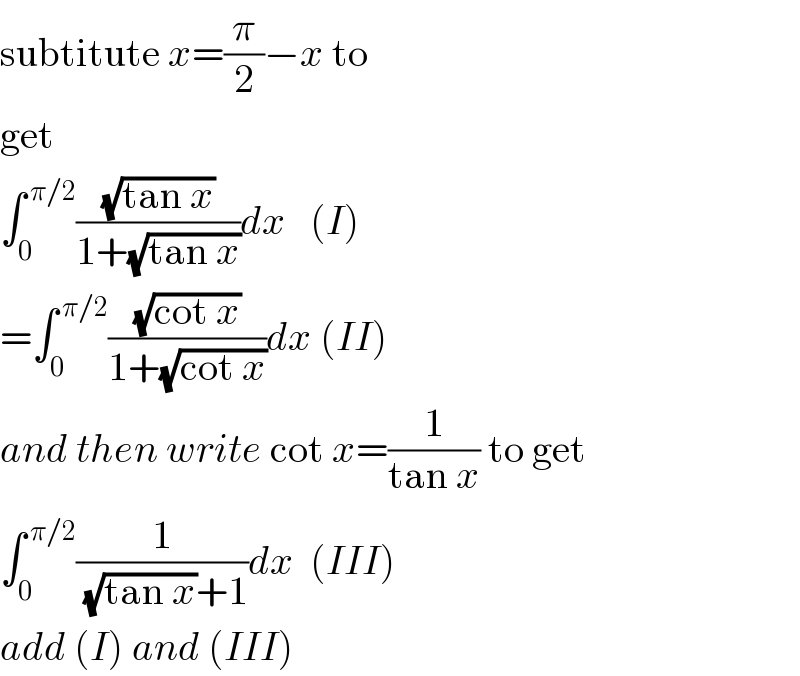
$$\mathrm{subtitute}\:{x}=\frac{\pi}{\mathrm{2}}−{x}\:\mathrm{to} \\ $$$$\mathrm{get} \\ $$$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}}{dx}\:\:\:\left({I}\right) \\ $$$$=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\sqrt{\mathrm{cot}\:{x}}}{\mathrm{1}+\sqrt{\mathrm{cot}\:{x}}}{dx}\:\left({II}\right) \\ $$$${and}\:{then}\:{write}\:\mathrm{cot}\:{x}=\frac{\mathrm{1}}{\mathrm{tan}\:{x}}\:\mathrm{to}\:\mathrm{get} \\ $$$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:{x}}+\mathrm{1}}{dx}\:\:\left({III}\right) \\ $$$${add}\:\left({I}\right)\:{and}\:\left({III}\right) \\ $$
Commented by Joel578 last updated on 05/Dec/17
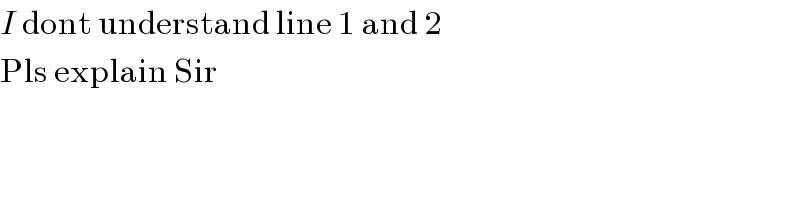
$${I}\:\mathrm{dont}\:\mathrm{understand}\:\mathrm{line}\:\mathrm{1}\:\mathrm{and}\:\mathrm{2} \\ $$$$\mathrm{Pls}\:\mathrm{explain}\:\mathrm{Sir} \\ $$
Commented by Joel578 last updated on 06/Dec/17
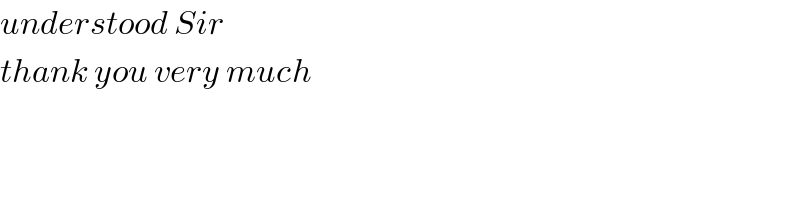
$${understood}\:{Sir} \\ $$$${thank}\:{you}\:{very}\:{much} \\ $$
