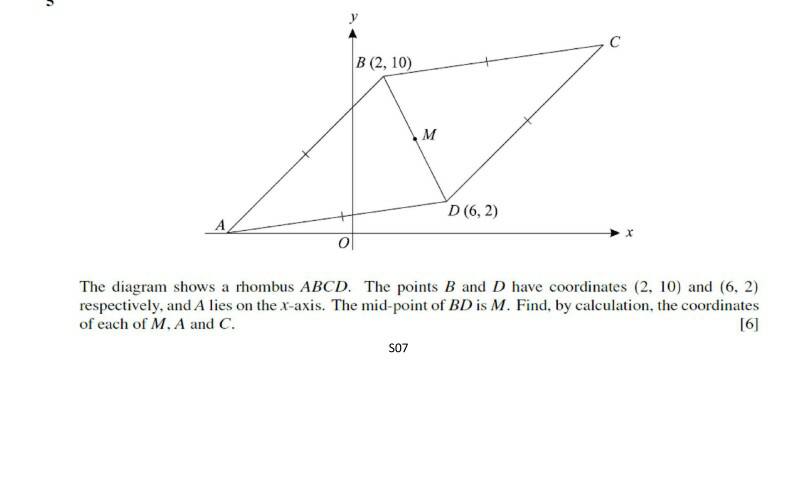
Question Number 25156 by tawa tawa last updated on 05/Dec/17
Answered by nnnavendu last updated on 05/Dec/17
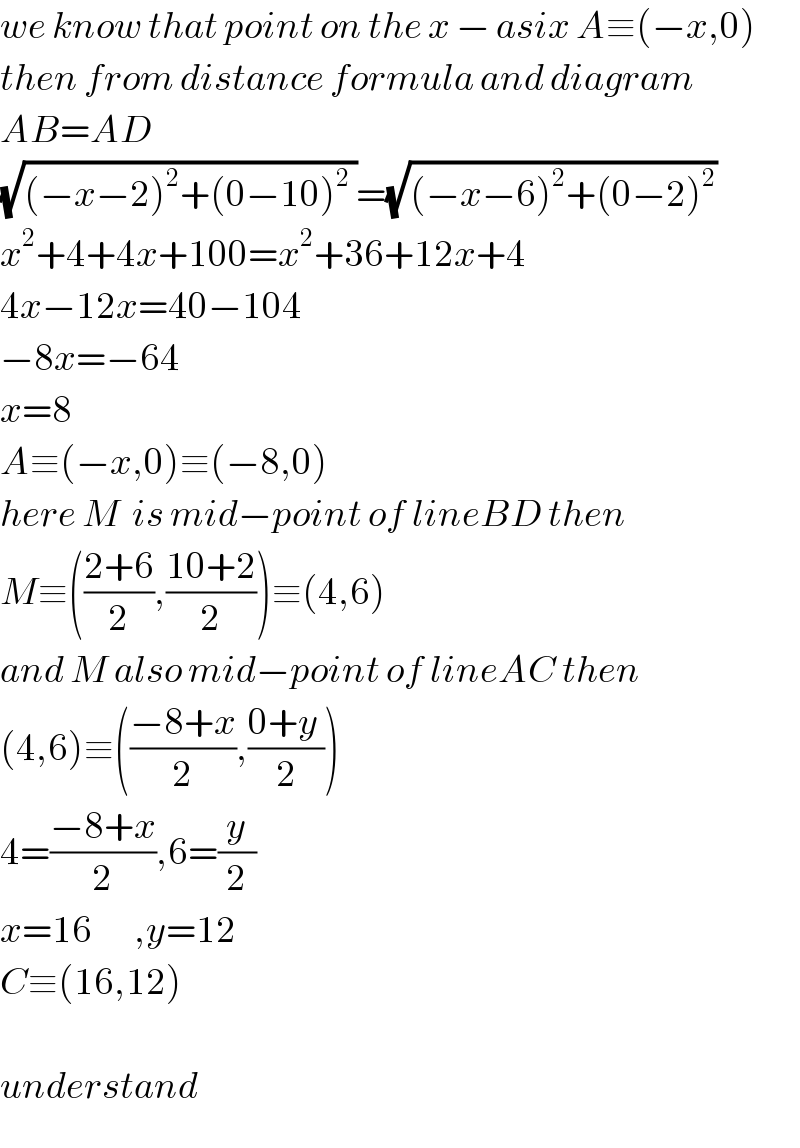
$${we}\:{know}\:{that}\:{point}\:{on}\:{the}\:{x}\:−\:{asix}\:{A}\equiv\left(−{x},\mathrm{0}\right) \\ $$$${then}\:{from}\:{distance}\:{formula}\:{and}\:{diagram} \\ $$$${AB}={AD} \\ $$$$\sqrt{\left(−{x}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{0}−\mathrm{10}\right)^{\mathrm{2}} \:}=\sqrt{\left(−{x}−\mathrm{6}\right)^{\mathrm{2}} +\left(\mathrm{0}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} +\mathrm{4}+\mathrm{4}{x}+\mathrm{100}={x}^{\mathrm{2}} +\mathrm{36}+\mathrm{12}{x}+\mathrm{4} \\ $$$$\mathrm{4}{x}−\mathrm{12}{x}=\mathrm{40}−\mathrm{104} \\ $$$$−\mathrm{8}{x}=−\mathrm{64} \\ $$$${x}=\mathrm{8} \\ $$$${A}\equiv\left(−{x},\mathrm{0}\right)\equiv\left(−\mathrm{8},\mathrm{0}\right) \\ $$$${here}\:{M}\:\:{is}\:{mid}−{point}\:{of}\:{lineBD}\:{then}\: \\ $$$${M}\equiv\left(\frac{\mathrm{2}+\mathrm{6}}{\mathrm{2}},\frac{\mathrm{10}+\mathrm{2}}{\mathrm{2}}\right)\equiv\left(\mathrm{4},\mathrm{6}\right) \\ $$$${and}\:{M}\:{also}\:{mid}−{point}\:{of}\:{lineAC}\:{then} \\ $$$$\left(\mathrm{4},\mathrm{6}\right)\equiv\left(\frac{−\mathrm{8}+{x}}{\mathrm{2}},\frac{\mathrm{0}+{y}\:}{\mathrm{2}}\right) \\ $$$$\mathrm{4}=\frac{−\mathrm{8}+{x}}{\mathrm{2}},\mathrm{6}=\frac{{y}}{\mathrm{2}} \\ $$$${x}=\mathrm{16}\:\:\:\:\:\:\:,{y}=\mathrm{12} \\ $$$${C}\equiv\left(\mathrm{16},\mathrm{12}\right)\: \\ $$$$ \\ $$$${understand}\: \\ $$
Commented by tawa tawa last updated on 05/Dec/17
$$\mathrm{very}\:\mathrm{well},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by nnnavendu last updated on 05/Dec/17

$${thanks}\: \\ $$
Answered by mrW1 last updated on 05/Dec/17
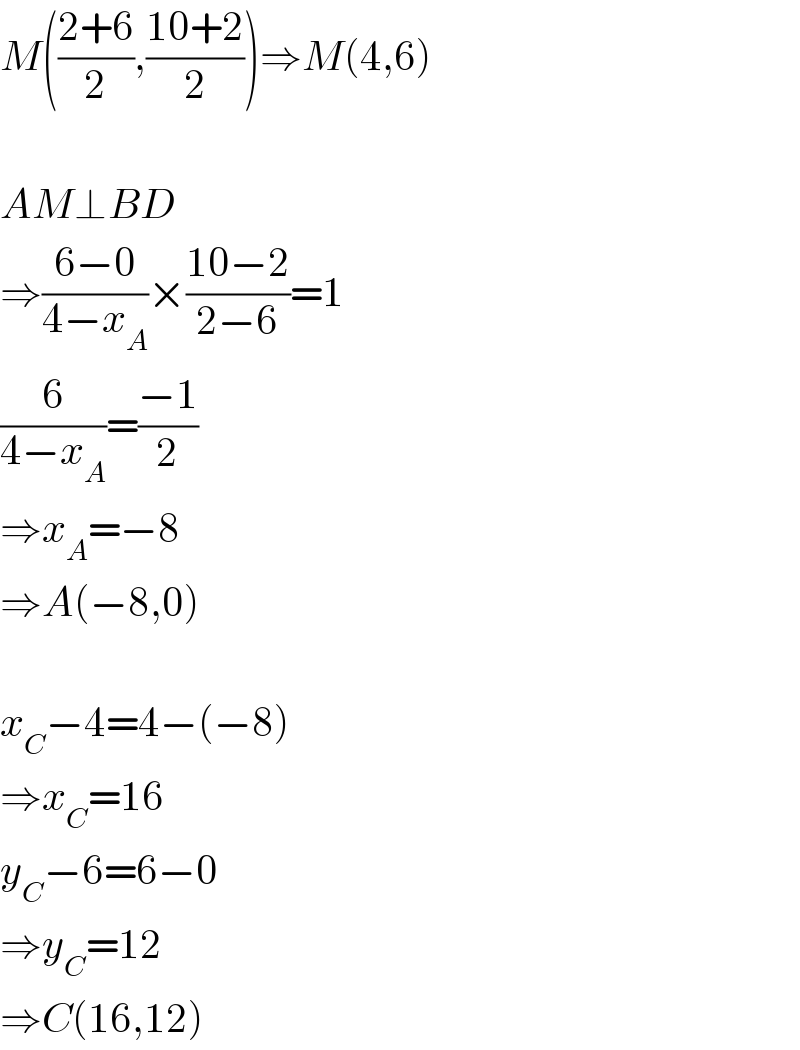
$${M}\left(\frac{\mathrm{2}+\mathrm{6}}{\mathrm{2}},\frac{\mathrm{10}+\mathrm{2}}{\mathrm{2}}\right)\Rightarrow{M}\left(\mathrm{4},\mathrm{6}\right) \\ $$$$ \\ $$$${AM}\bot{BD} \\ $$$$\Rightarrow\frac{\mathrm{6}−\mathrm{0}}{\mathrm{4}−{x}_{{A}} }×\frac{\mathrm{10}−\mathrm{2}}{\mathrm{2}−\mathrm{6}}=\mathrm{1} \\ $$$$\frac{\mathrm{6}}{\mathrm{4}−{x}_{{A}} }=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{A}} =−\mathrm{8} \\ $$$$\Rightarrow{A}\left(−\mathrm{8},\mathrm{0}\right) \\ $$$$ \\ $$$${x}_{{C}} −\mathrm{4}=\mathrm{4}−\left(−\mathrm{8}\right) \\ $$$$\Rightarrow{x}_{{C}} =\mathrm{16} \\ $$$${y}_{{C}} −\mathrm{6}=\mathrm{6}−\mathrm{0} \\ $$$$\Rightarrow{y}_{{C}} =\mathrm{12} \\ $$$$\Rightarrow{C}\left(\mathrm{16},\mathrm{12}\right) \\ $$
Commented by tawa tawa last updated on 05/Dec/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
