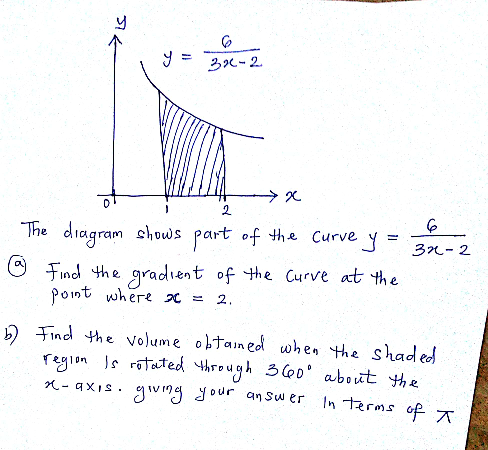
Question Number 25201 by tawa tawa last updated on 06/Dec/17
Answered by ajfour last updated on 06/Dec/17
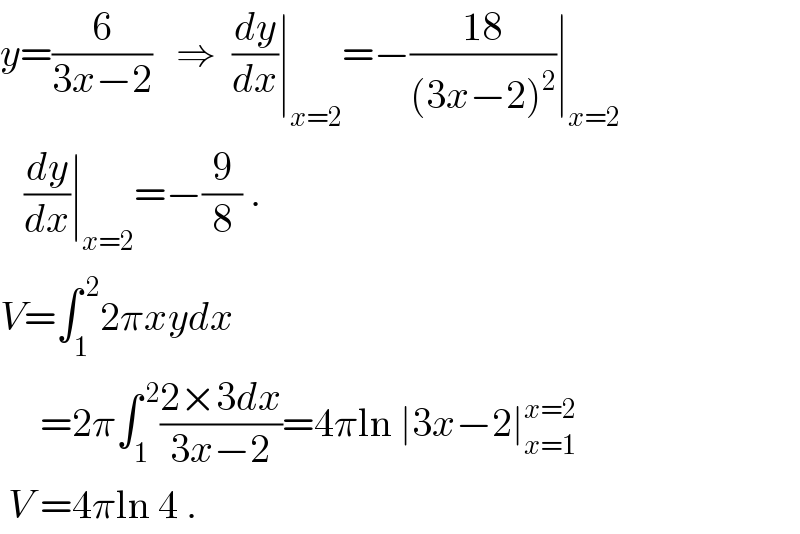
$${y}=\frac{\mathrm{6}}{\mathrm{3}{x}−\mathrm{2}}\:\:\:\Rightarrow\:\:\frac{{dy}}{{dx}}\mid_{{x}=\mathrm{2}} =−\frac{\mathrm{18}}{\left(\mathrm{3}{x}−\mathrm{2}\right)^{\mathrm{2}} }\mid_{{x}=\mathrm{2}} \\ $$$$\:\:\:\frac{{dy}}{{dx}}\mid_{{x}=\mathrm{2}} =−\frac{\mathrm{9}}{\mathrm{8}}\:. \\ $$$${V}=\int_{\mathrm{1}} ^{\:\mathrm{2}} \mathrm{2}\pi{xydx}\: \\ $$$$\:\:\:\:\:=\mathrm{2}\pi\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{2}×\mathrm{3}{dx}}{\mathrm{3}{x}−\mathrm{2}}=\mathrm{4}\pi\mathrm{ln}\:\mid\mathrm{3}{x}−\mathrm{2}\mid_{{x}=\mathrm{1}} ^{{x}=\mathrm{2}} \\ $$$$\:{V}\:=\mathrm{4}\pi\mathrm{ln}\:\mathrm{4}\:. \\ $$
Commented by tawa tawa last updated on 06/Dec/17

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by mrW1 last updated on 06/Dec/17
![ajfour sir, please check: it should be a rotation about x−axis. V=∫_1 ^( 2) πy^2 dx ⇒V=π∫_1 ^( 2) ((36)/((3x−2)^2 ))dx ⇒V=12π∫_1 ^( 2) (1/((3x−2)^2 ))d(3x) ⇒V=12π[−(1/(3x−2))]_1 ^2 ⇒V=12π((1/1)−(1/4)) ⇒V=9π](https://www.tinkutara.com/question/Q25233.png)
$${ajfour}\:{sir},\:{please}\:{check}: \\ $$$${it}\:{should}\:{be}\:{a}\:{rotation}\:{about}\:{x}−{axis}. \\ $$$$ \\ $$$${V}=\int_{\mathrm{1}} ^{\:\mathrm{2}} \pi{y}^{\mathrm{2}} {dx}\: \\ $$$$\Rightarrow{V}=\pi\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{36}}{\left(\mathrm{3}{x}−\mathrm{2}\right)^{\mathrm{2}} }{dx}\: \\ $$$$\Rightarrow{V}=\mathrm{12}\pi\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{\left(\mathrm{3}{x}−\mathrm{2}\right)^{\mathrm{2}} }{d}\left(\mathrm{3}{x}\right)\: \\ $$$$\Rightarrow{V}=\mathrm{12}\pi\left[−\frac{\mathrm{1}}{\mathrm{3}{x}−\mathrm{2}}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow{V}=\mathrm{12}\pi\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\Rightarrow{V}=\mathrm{9}\pi \\ $$
Commented by tawa tawa last updated on 06/Dec/17

$$\mathrm{Yes}\:\mathrm{9}\pi\:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:\mathrm{options}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
