Question Number 25367 by ajfour last updated on 08/Dec/17
Commented by ajfour last updated on 08/Dec/17
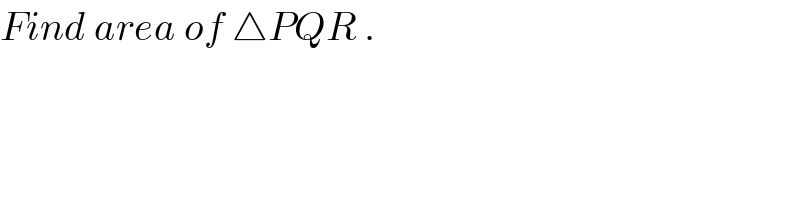
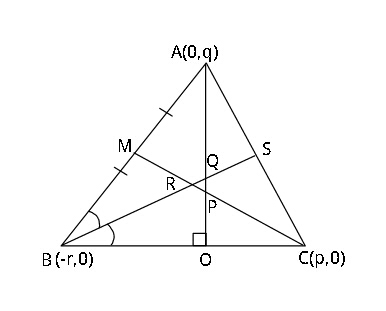
$${Find}\:{area}\:{of}\:\bigtriangleup{PQR}\:. \\ $$
Answered by jota+ last updated on 09/Dec/17
![let ∡QBO=∡ABQ=θ point Q. Q (0, rtan θ) point P. M(−r/2, q/2) equation of MC y=((q/2−0)/(−r/2−p)) (x−p) ...(1) P(0, ((pq)/(r+2p))) point R. R=BQ ∤ MC equation of BQ y=tan θ(x+r) ...(2) resolving (1) and (2) R(((y_P −y_Q )/(tan θ+m)), ((y_P −y_Q )/(1+m/tan θ)) +y_Q ) where m=(q/(r+2p)) Area= ((abs[x_R (y_Q −y_P )])/2) =(((y_Q −y_P )^2 )/(2(tan θ+m))).](https://www.tinkutara.com/question/Q25389.png)
$${let}\:\measuredangle{QBO}=\measuredangle{ABQ}=\theta \\ $$$$ \\ $$$${point}\:{Q}.\:\:{Q}\:\left(\mathrm{0},\:\:{r}\mathrm{tan}\:\theta\right) \\ $$$$ \\ $$$${point}\:{P}.\:\:{M}\left(−{r}/\mathrm{2},\:{q}/\mathrm{2}\right) \\ $$$${equation}\:{of}\:{MC} \\ $$$${y}=\frac{{q}/\mathrm{2}−\mathrm{0}}{−{r}/\mathrm{2}−{p}}\:\left({x}−{p}\right)\:\:\:…\left(\mathrm{1}\right) \\ $$$${P}\left(\mathrm{0},\:\:\frac{{pq}}{{r}+\mathrm{2}{p}}\right)\: \\ $$$$ \\ $$$${point}\:{R}.\:\:{R}={BQ}\:\nmid\:{MC} \\ $$$${equation}\:{of}\:{BQ} \\ $$$${y}=\mathrm{tan}\:\theta\left({x}+{r}\right)\:\:\:\:\:\:…\left(\mathrm{2}\right) \\ $$$${resolving}\:\:\left(\mathrm{1}\right)\:{and}\:\:\left(\mathrm{2}\right) \\ $$$$\:\:{R}\left(\frac{{y}_{{P}} −{y}_{{Q}} \:}{\mathrm{tan}\:\theta+{m}},\:\frac{{y}_{{P}} −{y}_{{Q}} }{\mathrm{1}+{m}/\mathrm{tan}\:\theta}\:+{y}_{{Q}} \right) \\ $$$${where}\:{m}=\frac{{q}}{{r}+\mathrm{2}{p}} \\ $$$${Area}=\:\frac{{abs}\left[{x}_{{R}} \left({y}_{{Q}} −{y}_{{P}} \right)\right]}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({y}_{{Q}} −{y}_{{P}} \right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{tan}\:\theta+{m}\right)}. \\ $$
Commented by ajfour last updated on 10/Dec/17

$${thanks}. \\ $$
