Question-25460

Question Number 25460 by San Sophanethsan069 last updated on 10/Dec/17

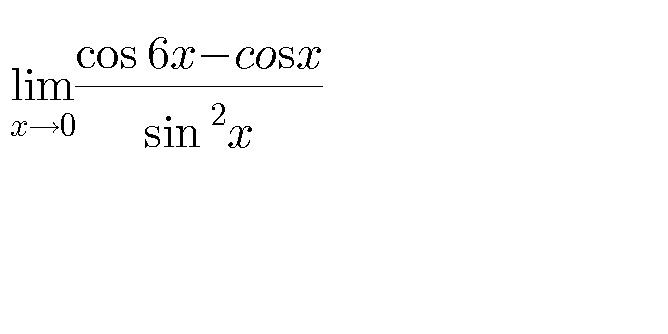
Commented by behi.8.3.4.17@gmail.com last updated on 10/Dec/17

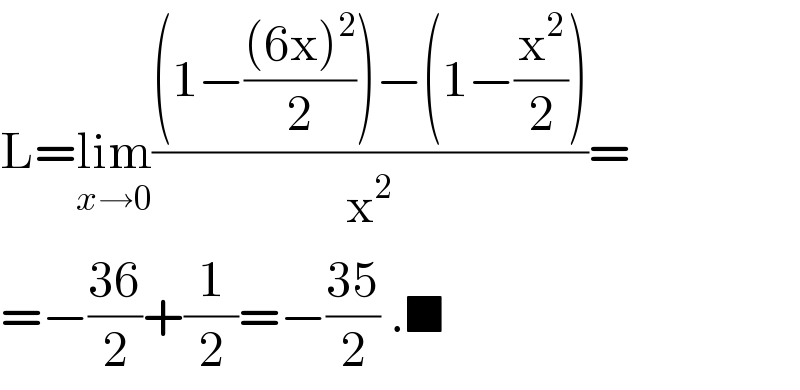
L=lim_(x→0) (((1−(((6x)^2 )/2))−(1−(x^2 /2)))/x^2 )= =−((36)/2)+(1/2)=−((35)/2) .■

$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}−\frac{\left(\mathrm{6x}\right)^{\mathrm{2}} }{\mathrm{2}}\right)−\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{x}^{\mathrm{2}} }= \\ $$$$=−\frac{\mathrm{36}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{35}}{\mathrm{2}}\:.\blacksquare \\ $$

Commented by San Sophanethsan069 last updated on 11/Dec/17

$$\mathrm{Thanks}\:\mathrm{you}. \\ $$

Answered by prakash jain last updated on 10/Dec/17

L′hospital rule lim_(x→0) ((cos 6x−cos x)/(sin^2 x)) =lim_(x→0) (((d/dx)(cos 6x−cos x))/((d/dx)sin^2 x)) =lim_(x→0) ((−6sin 6x+sin x)/(2sin xcos x)) =lim_(x→0) ((−6sin 6x+sin x)/(sin 2x)) =lim_(x→0) ((−6sin 6x)/(sin 2x))+lim_(x→0) ((sin x)/(sin 2x)) =lim_(x→0) ((−36sin 6x)/(6x))∙((2x)/(2sin 2x))+lim_(x→0) ((sin x)/x)∙((2x)/(2sin 2x)) =(−36)×(1/2)+(1/2)=−18+(1/2)=−((35)/2)

$$\mathrm{L}'\mathrm{hospital}\:\mathrm{rule} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{6}{x}−\mathrm{cos}\:{x}}{\mathrm{sin}^{\mathrm{2}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left(\mathrm{cos}\:\mathrm{6}{x}−\mathrm{cos}\:{x}\right)}{\frac{{d}}{{dx}}\mathrm{sin}^{\mathrm{2}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{6sin}\:\mathrm{6}{x}+\mathrm{sin}\:{x}}{\mathrm{2sin}\:{x}\mathrm{cos}\:{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{6sin}\:\mathrm{6}{x}+\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{6sin}\:\mathrm{6}{x}}{\mathrm{sin}\:\mathrm{2}{x}}+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{36sin}\:\mathrm{6}{x}}{\mathrm{6}{x}}\centerdot\frac{\mathrm{2}{x}}{\mathrm{2sin}\:\mathrm{2}{x}}+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}}{{x}}\centerdot\frac{\mathrm{2}{x}}{\mathrm{2sin}\:\mathrm{2}{x}} \\ $$$$=\left(−\mathrm{36}\right)×\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=−\mathrm{18}+\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{35}}{\mathrm{2}} \\ $$

Commented by San Sophanethsan069 last updated on 11/Dec/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply