Question Number 25488 by Mahesh Andiboina last updated on 11/Dec/17
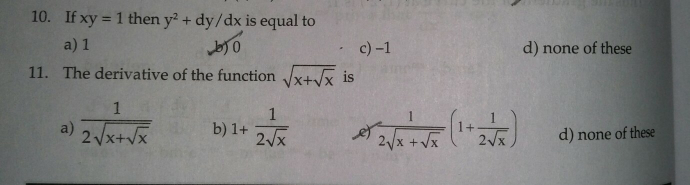
Commented by prakash jain last updated on 11/Dec/17
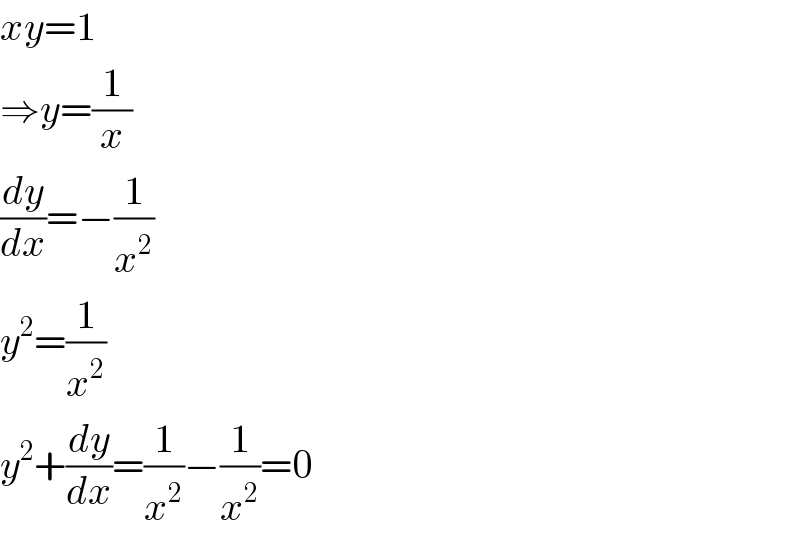
$${xy}=\mathrm{1} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} +\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$
Commented by Mahesh Andiboina last updated on 11/Dec/17

$$\mathrm{thnk}\:\mathrm{u}\:\mathrm{ji} \\ $$
Commented by Mahesh Andiboina last updated on 11/Dec/17

$$\mathrm{plzzz}….\:\mathrm{also}\:\mathrm{ans}\:\mathrm{the}\:\mathrm{q}\:\mathrm{no}\:\mathrm{11} \\ $$
Answered by rita1608 last updated on 11/Dec/17
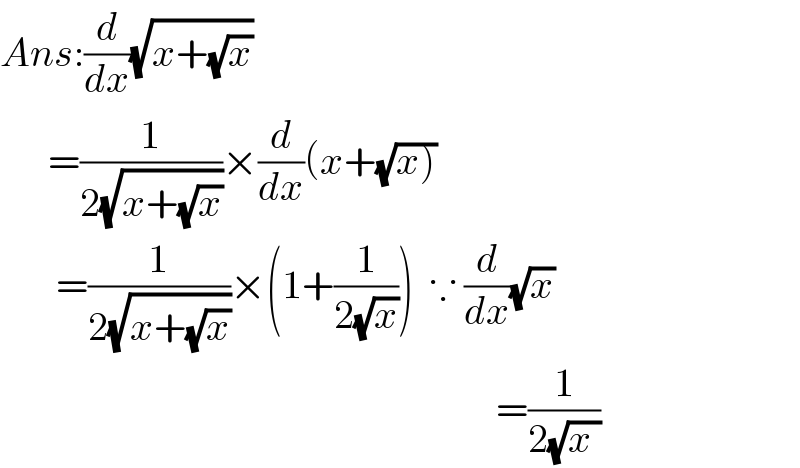
$${Ans}:\frac{{d}}{{dx}}\sqrt{{x}+\sqrt{{x}}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}}}}×\frac{{d}}{{dx}}\left({x}+\sqrt{\left.{x}\right)}\right. \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}}}}×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right)\:\:\because\:\frac{{d}}{{dx}}\sqrt{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}\:}} \\ $$
Answered by prakash jain last updated on 11/Dec/17
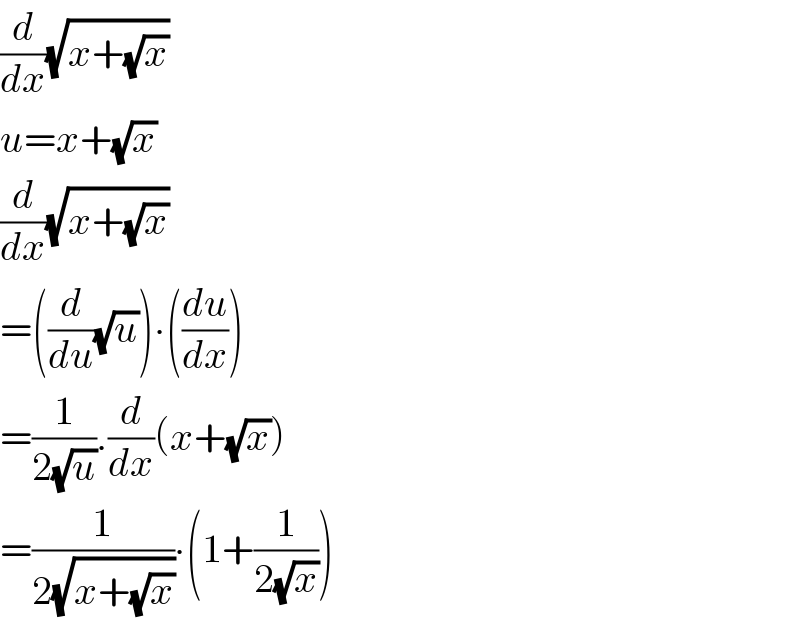
$$\frac{{d}}{{dx}}\sqrt{{x}+\sqrt{{x}}} \\ $$$${u}={x}+\sqrt{{x}} \\ $$$$\frac{{d}}{{dx}}\sqrt{{x}+\sqrt{{x}}} \\ $$$$=\left(\frac{{d}}{{du}}\sqrt{{u}}\right)\centerdot\left(\frac{{du}}{{dx}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{u}}}.\frac{{d}}{{dx}}\left({x}+\sqrt{{x}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}}}}\centerdot\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right) \\ $$
Commented by Mahesh Andiboina last updated on 11/Dec/17

$$\mathrm{thnq} \\ $$
