Question Number 25619 by aplus last updated on 12/Dec/17

Answered by prakash jain last updated on 12/Dec/17
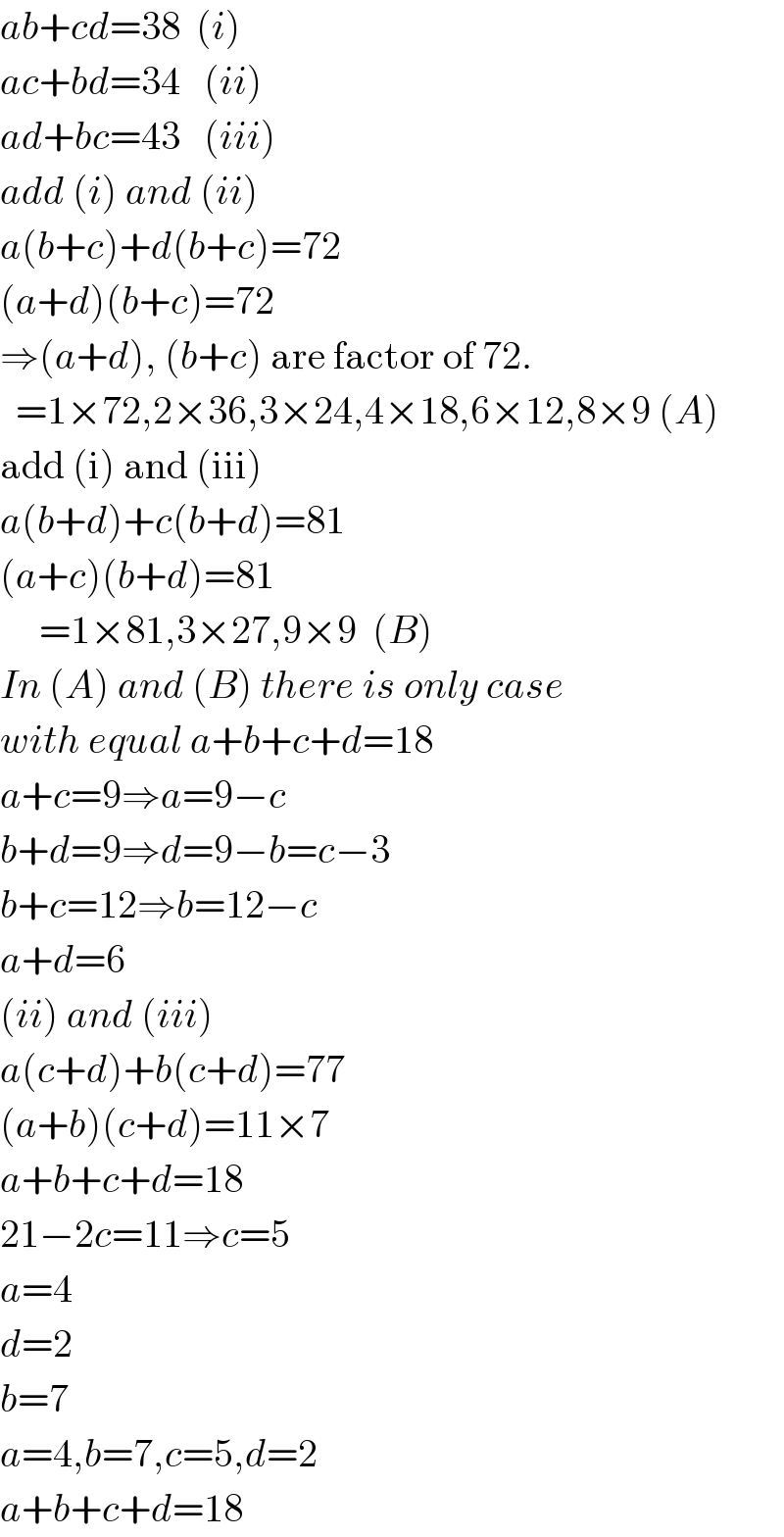
$${ab}+{cd}=\mathrm{38}\:\:\left({i}\right) \\ $$$${ac}+{bd}=\mathrm{34}\:\:\:\left({ii}\right) \\ $$$${ad}+{bc}=\mathrm{43}\:\:\:\left({iii}\right) \\ $$$${add}\:\left({i}\right)\:{and}\:\left({ii}\right) \\ $$$${a}\left({b}+{c}\right)+{d}\left({b}+{c}\right)=\mathrm{72} \\ $$$$\left({a}+{d}\right)\left({b}+{c}\right)=\mathrm{72} \\ $$$$\Rightarrow\left({a}+{d}\right),\:\left({b}+{c}\right)\:\mathrm{are}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{72}. \\ $$$$\:\:=\mathrm{1}×\mathrm{72},\mathrm{2}×\mathrm{36},\mathrm{3}×\mathrm{24},\mathrm{4}×\mathrm{18},\mathrm{6}×\mathrm{12},\mathrm{8}×\mathrm{9}\:\left({A}\right) \\ $$$$\mathrm{add}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{iii}\right) \\ $$$${a}\left({b}+{d}\right)+{c}\left({b}+{d}\right)=\mathrm{81} \\ $$$$\left({a}+{c}\right)\left({b}+{d}\right)=\mathrm{81} \\ $$$$\:\:\:\:\:=\mathrm{1}×\mathrm{81},\mathrm{3}×\mathrm{27},\mathrm{9}×\mathrm{9}\:\:\left({B}\right) \\ $$$${In}\:\left({A}\right)\:{and}\:\left({B}\right)\:{there}\:{is}\:{only}\:{case} \\ $$$${with}\:{equal}\:{a}+{b}+{c}+{d}=\mathrm{18} \\ $$$${a}+{c}=\mathrm{9}\Rightarrow{a}=\mathrm{9}−{c} \\ $$$${b}+{d}=\mathrm{9}\Rightarrow{d}=\mathrm{9}−{b}={c}−\mathrm{3} \\ $$$${b}+{c}=\mathrm{12}\Rightarrow{b}=\mathrm{12}−{c} \\ $$$${a}+{d}=\mathrm{6} \\ $$$$\left({ii}\right)\:{and}\:\left({iii}\right) \\ $$$${a}\left({c}+{d}\right)+{b}\left({c}+{d}\right)=\mathrm{77} \\ $$$$\left({a}+{b}\right)\left({c}+{d}\right)=\mathrm{11}×\mathrm{7} \\ $$$${a}+{b}+{c}+{d}=\mathrm{18} \\ $$$$\mathrm{21}−\mathrm{2}{c}=\mathrm{11}\Rightarrow{c}=\mathrm{5} \\ $$$${a}=\mathrm{4} \\ $$$${d}=\mathrm{2} \\ $$$${b}=\mathrm{7} \\ $$$${a}=\mathrm{4},{b}=\mathrm{7},{c}=\mathrm{5},{d}=\mathrm{2} \\ $$$${a}+{b}+{c}+{d}=\mathrm{18} \\ $$
