Question Number 25675 by naka3546 last updated on 12/Dec/17
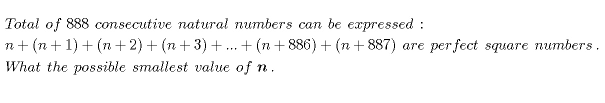
Commented by moxhix last updated on 12/Dec/17
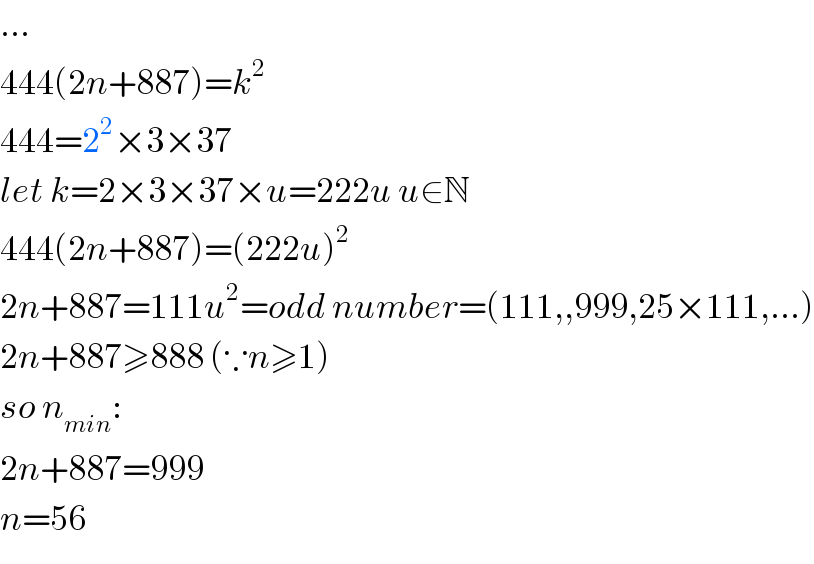
$$… \\ $$$$\mathrm{444}\left(\mathrm{2}{n}+\mathrm{887}\right)={k}^{\mathrm{2}} \\ $$$$\mathrm{444}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3}×\mathrm{37} \\ $$$${let}\:{k}=\mathrm{2}×\mathrm{3}×\mathrm{37}×{u}=\mathrm{222}{u}\:{u}\in\mathbb{N} \\ $$$$\mathrm{444}\left(\mathrm{2}{n}+\mathrm{887}\right)=\left(\mathrm{222}{u}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{n}+\mathrm{887}=\mathrm{111}{u}^{\mathrm{2}} ={odd}\:{number}=\left(\mathrm{111},,\mathrm{999},\mathrm{25}×\mathrm{111},…\right) \\ $$$$\mathrm{2}{n}+\mathrm{887}\geqslant\mathrm{888}\:\left(\because{n}\geqslant\mathrm{1}\right) \\ $$$${so}\:{n}_{{min}} : \\ $$$$\mathrm{2}{n}+\mathrm{887}=\mathrm{999} \\ $$$${n}=\mathrm{56} \\ $$
Answered by mrW1 last updated on 12/Dec/17
![S=((888×(2n+887))/2)=k^2 444×(2n+887)=k^2 3×37×(2n+887)=((k/2))^2 2n+887=3×37×m^2 n=((3×37×m^2 −887)/2) m must be odd and m≥(√((887)/(3×37)))≈2.8 the min. m=3 ⇒min. n=((3×37×9−887)/2)=56 56+57+...+943=666^2 in general m=2i+1, i≥1 n=((3×37×(2i+1)^2 −887)/2) n=2×[111i(i+1)−194] n=56, 994, 2276, 4052, ......](https://www.tinkutara.com/question/Q25679.png)
$${S}=\frac{\mathrm{888}×\left(\mathrm{2}{n}+\mathrm{887}\right)}{\mathrm{2}}={k}^{\mathrm{2}} \\ $$$$\mathrm{444}×\left(\mathrm{2}{n}+\mathrm{887}\right)={k}^{\mathrm{2}} \\ $$$$\mathrm{3}×\mathrm{37}×\left(\mathrm{2}{n}+\mathrm{887}\right)=\left(\frac{{k}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{n}+\mathrm{887}=\mathrm{3}×\mathrm{37}×{m}^{\mathrm{2}} \\ $$$${n}=\frac{\mathrm{3}×\mathrm{37}×{m}^{\mathrm{2}} −\mathrm{887}}{\mathrm{2}} \\ $$$${m}\:{must}\:{be}\:{odd}\:{and} \\ $$$${m}\geqslant\sqrt{\frac{\mathrm{887}}{\mathrm{3}×\mathrm{37}}}\approx\mathrm{2}.\mathrm{8} \\ $$$${the}\:{min}.\:{m}=\mathrm{3} \\ $$$$\Rightarrow{min}.\:{n}=\frac{\mathrm{3}×\mathrm{37}×\mathrm{9}−\mathrm{887}}{\mathrm{2}}=\mathrm{56} \\ $$$$ \\ $$$$\mathrm{56}+\mathrm{57}+…+\mathrm{943}=\mathrm{666}^{\mathrm{2}} \\ $$$$ \\ $$$${in}\:{general}\:{m}=\mathrm{2}{i}+\mathrm{1},\:{i}\geqslant\mathrm{1} \\ $$$${n}=\frac{\mathrm{3}×\mathrm{37}×\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{887}}{\mathrm{2}} \\ $$$${n}=\mathrm{2}×\left[\mathrm{111}{i}\left({i}+\mathrm{1}\right)−\mathrm{194}\right] \\ $$$${n}=\mathrm{56},\:\mathrm{994},\:\mathrm{2276},\:\mathrm{4052},\:…… \\ $$
