Question Number 25712 by ajfour last updated on 13/Dec/17

Commented by ajfour last updated on 13/Dec/17

$${solution}\:{to}\:{Q}.\mathrm{25706} \\ $$
Answered by ajfour last updated on 13/Dec/17
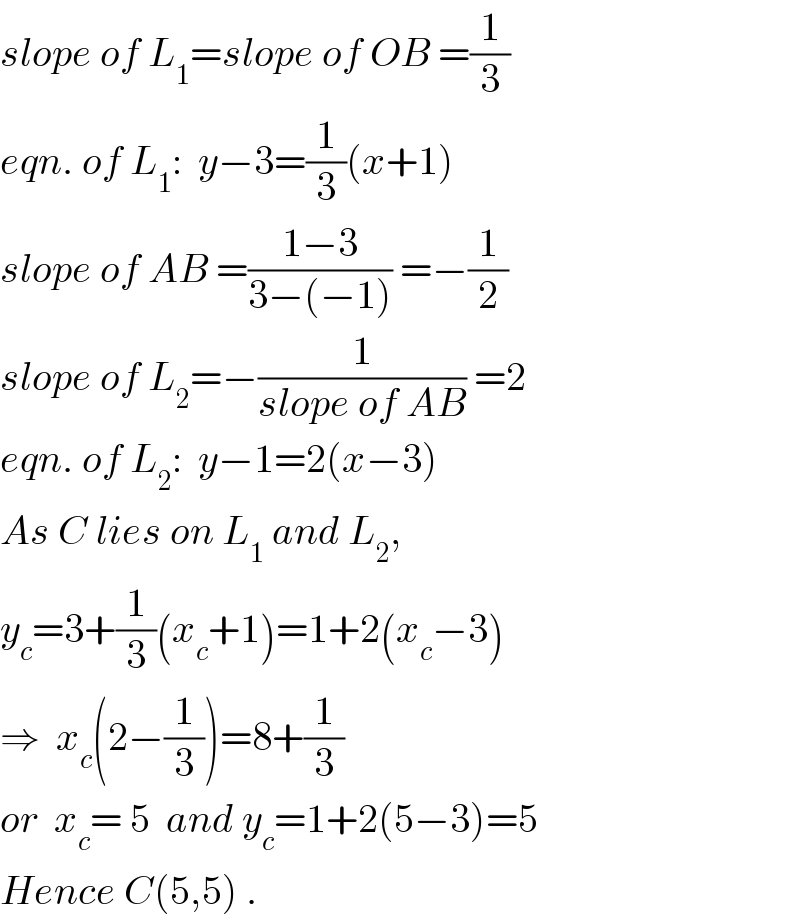
$${slope}\:{of}\:{L}_{\mathrm{1}} ={slope}\:{of}\:{OB}\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${eqn}.\:{of}\:{L}_{\mathrm{1}} :\:\:{y}−\mathrm{3}=\frac{\mathrm{1}}{\mathrm{3}}\left({x}+\mathrm{1}\right) \\ $$$${slope}\:{of}\:{AB}\:=\frac{\mathrm{1}−\mathrm{3}}{\mathrm{3}−\left(−\mathrm{1}\right)}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${slope}\:{of}\:{L}_{\mathrm{2}} =−\frac{\mathrm{1}}{{slope}\:{of}\:{AB}}\:=\mathrm{2} \\ $$$${eqn}.\:{of}\:{L}_{\mathrm{2}} :\:\:{y}−\mathrm{1}=\mathrm{2}\left({x}−\mathrm{3}\right) \\ $$$${As}\:{C}\:{lies}\:{on}\:{L}_{\mathrm{1}} \:{and}\:{L}_{\mathrm{2}} , \\ $$$${y}_{{c}} =\mathrm{3}+\frac{\mathrm{1}}{\mathrm{3}}\left({x}_{{c}} +\mathrm{1}\right)=\mathrm{1}+\mathrm{2}\left({x}_{{c}} −\mathrm{3}\right) \\ $$$$\Rightarrow\:\:{x}_{{c}} \left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{8}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${or}\:\:{x}_{{c}} =\:\mathrm{5}\:\:{and}\:{y}_{{c}} =\mathrm{1}+\mathrm{2}\left(\mathrm{5}−\mathrm{3}\right)=\mathrm{5} \\ $$$${Hence}\:{C}\left(\mathrm{5},\mathrm{5}\right)\:. \\ $$
Commented by tawa tawa last updated on 13/Dec/17
$$\mathrm{Wow}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 13/Dec/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Now}\:\mathrm{i}\:\mathrm{understand}. \\ $$
Commented by tawa tawa last updated on 13/Dec/17
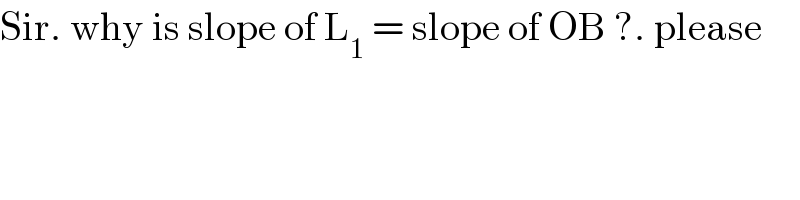
$$\mathrm{Sir}.\:\mathrm{why}\:\mathrm{is}\:\mathrm{slope}\:\mathrm{of}\:\mathrm{L}_{\mathrm{1}} \:=\:\mathrm{slope}\:\mathrm{of}\:\mathrm{OB}\:?.\:\mathrm{please} \\ $$
Commented by ajfour last updated on 13/Dec/17
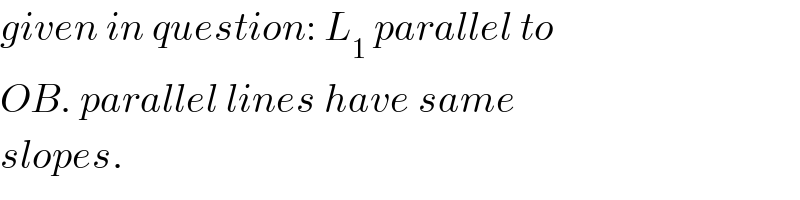
$${given}\:{in}\:{question}:\:{L}_{\mathrm{1}} \:{parallel}\:{to} \\ $$$${OB}.\:{parallel}\:{lines}\:{have}\:{same} \\ $$$${slopes}. \\ $$
