Question Number 25728 by ajfour last updated on 13/Dec/17
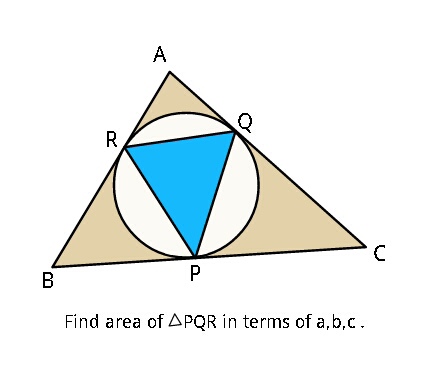
Commented by ajfour last updated on 13/Dec/17

$${If}\:{ratio}\:{of}\:{areas}\:{of}\:\bigtriangleup{PQR}\:{and} \\ $$$$\bigtriangleup{ABC}\:{be}\:{independent}\:{of}\:{a},{b},{c}\:; \\ $$$${find}\:{the}\:{ratio}. \\ $$
Commented by behi.8.3.4.17@gmail.com last updated on 14/Dec/17

Commented by mrW1 last updated on 14/Dec/17

$${very}\:{nice}! \\ $$
Answered by mrW1 last updated on 13/Dec/17
![let BC=a and RQ=a′ etc. AR=AQ=((b+c−a)/2) a^2 =b^2 +c^2 −2bc cos A a′^2 =2(((b+c−a)/2))^2 [1−cos A] =(((b+c−a)^2 )/2)[1−((b^2 +c^2 −a^2 )/(2bc))] =(((b+c−a)^2 )/2)[((a^2 −(b−c)^2 )/(2bc))] =(((b+c−a)^2 (a+b−c)(a+c−b))/(4bc)) ⇒a′=(1/2)(√(((b+c−a)^2 (a+b−c)(a+c−b))/(bc))) ⇒a′=2(s−a)(√(((s−c)(s−b))/(bc))) ⇒a′=2(s−a)(√(((s/b)−1)((s/c)−1))) ⇒b′=2(s−b)(√(((s/a)−1)((s/c)−1))) ⇒c′=2(s−c)(√(((s/a)−1)((s/b)−1))) with s=((a+b+c)/2) and s′=((a′+b′+c′)/2) ⇒A_(PQR) =(√(s′(s′−a)(s′−b′)(s′−c′)))](https://www.tinkutara.com/question/Q25751.png)
$${let}\:{BC}={a}\:{and}\:{RQ}={a}'\:{etc}. \\ $$$${AR}={AQ}=\frac{{b}+{c}−{a}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\mathrm{cos}\:{A} \\ $$$${a}'^{\mathrm{2}} =\mathrm{2}\left(\frac{{b}+{c}−{a}}{\mathrm{2}}\right)^{\mathrm{2}} \left[\mathrm{1}−\mathrm{cos}\:{A}\right] \\ $$$$=\frac{\left({b}+{c}−{a}\right)^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{1}−\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}\right] \\ $$$$=\frac{\left({b}+{c}−{a}\right)^{\mathrm{2}} }{\mathrm{2}}\left[\frac{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} }{\mathrm{2}{bc}}\right] \\ $$$$=\frac{\left({b}+{c}−{a}\right)^{\mathrm{2}} \left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)}{\mathrm{4}{bc}} \\ $$$$\Rightarrow{a}'=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left({b}+{c}−{a}\right)^{\mathrm{2}} \left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)}{{bc}}} \\ $$$$\Rightarrow{a}'=\mathrm{2}\left({s}−{a}\right)\sqrt{\frac{\left({s}−{c}\right)\left({s}−{b}\right)}{{bc}}} \\ $$$$\Rightarrow{a}'=\mathrm{2}\left({s}−{a}\right)\sqrt{\left(\frac{{s}}{{b}}−\mathrm{1}\right)\left(\frac{{s}}{{c}}−\mathrm{1}\right)} \\ $$$$\Rightarrow{b}'=\mathrm{2}\left({s}−{b}\right)\sqrt{\left(\frac{{s}}{{a}}−\mathrm{1}\right)\left(\frac{{s}}{{c}}−\mathrm{1}\right)} \\ $$$$\Rightarrow{c}'=\mathrm{2}\left({s}−{c}\right)\sqrt{\left(\frac{{s}}{{a}}−\mathrm{1}\right)\left(\frac{{s}}{{b}}−\mathrm{1}\right)} \\ $$$${with}\:{s}=\frac{{a}+{b}+{c}}{\mathrm{2}}\:{and} \\ $$$${s}'=\frac{{a}'+{b}'+{c}'}{\mathrm{2}} \\ $$$$\Rightarrow{A}_{{PQR}} =\sqrt{{s}'\left({s}'−{a}\right)\left({s}'−{b}'\right)\left({s}'−{c}'\right)} \\ $$
Commented by ajfour last updated on 14/Dec/17
$${please}\:{explain}\:{line}\:\mathrm{2}\:{Sir}.. \\ $$
Commented by mrW1 last updated on 14/Dec/17
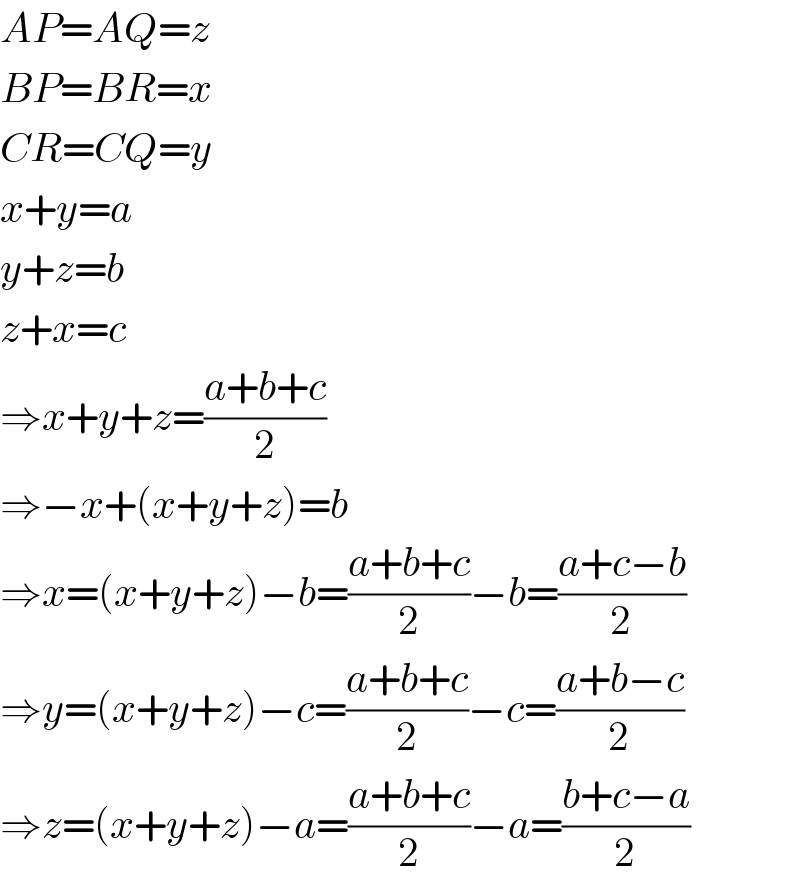
$${AP}={AQ}={z} \\ $$$${BP}={BR}={x} \\ $$$${CR}={CQ}={y} \\ $$$${x}+{y}={a} \\ $$$${y}+{z}={b} \\ $$$${z}+{x}={c} \\ $$$$\Rightarrow{x}+{y}+{z}=\frac{{a}+{b}+{c}}{\mathrm{2}} \\ $$$$\Rightarrow−{x}+\left({x}+{y}+{z}\right)={b} \\ $$$$\Rightarrow{x}=\left({x}+{y}+{z}\right)−{b}=\frac{{a}+{b}+{c}}{\mathrm{2}}−{b}=\frac{{a}+{c}−{b}}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\left({x}+{y}+{z}\right)−{c}=\frac{{a}+{b}+{c}}{\mathrm{2}}−{c}=\frac{{a}+{b}−{c}}{\mathrm{2}} \\ $$$$\Rightarrow{z}=\left({x}+{y}+{z}\right)−{a}=\frac{{a}+{b}+{c}}{\mathrm{2}}−{a}=\frac{{b}+{c}−{a}}{\mathrm{2}} \\ $$
