Question Number 25767 by tawa tawa last updated on 14/Dec/17

Answered by mrW1 last updated on 15/Dec/17
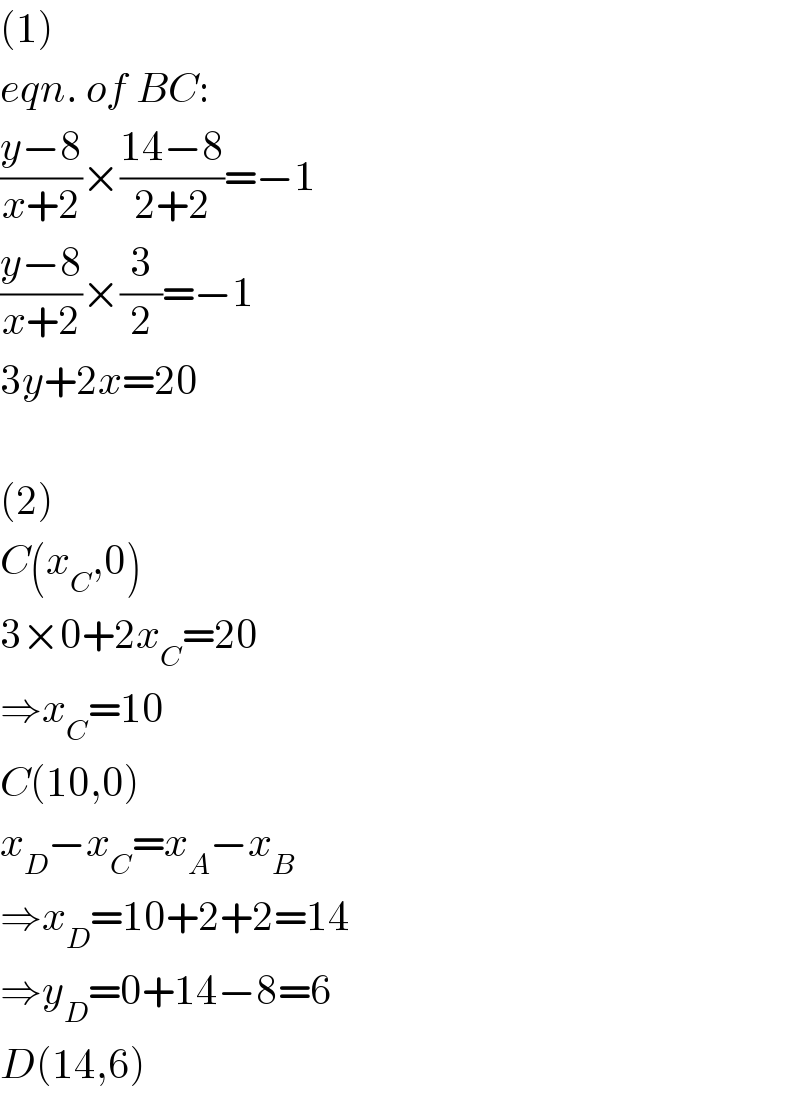
$$\left(\mathrm{1}\right) \\ $$$${eqn}.\:{of}\:{BC}: \\ $$$$\frac{{y}−\mathrm{8}}{{x}+\mathrm{2}}×\frac{\mathrm{14}−\mathrm{8}}{\mathrm{2}+\mathrm{2}}=−\mathrm{1} \\ $$$$\frac{{y}−\mathrm{8}}{{x}+\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{2}}=−\mathrm{1} \\ $$$$\mathrm{3}{y}+\mathrm{2}{x}=\mathrm{20} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${C}\left({x}_{{C}} ,\mathrm{0}\right) \\ $$$$\mathrm{3}×\mathrm{0}+\mathrm{2}{x}_{{C}} =\mathrm{20} \\ $$$$\Rightarrow{x}_{{C}} =\mathrm{10} \\ $$$${C}\left(\mathrm{10},\mathrm{0}\right) \\ $$$${x}_{{D}} −{x}_{{C}} ={x}_{{A}} −{x}_{{B}} \\ $$$$\Rightarrow{x}_{{D}} =\mathrm{10}+\mathrm{2}+\mathrm{2}=\mathrm{14} \\ $$$$\Rightarrow{y}_{{D}} =\mathrm{0}+\mathrm{14}−\mathrm{8}=\mathrm{6} \\ $$$${D}\left(\mathrm{14},\mathrm{6}\right) \\ $$
Commented by tawa tawa last updated on 15/Dec/17

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}:\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
