Menu Close

Question-25842

Tinku Tara 0 Comments
Pin




Question Number 25842 by Tinkutara last updated on 15/Dec/17
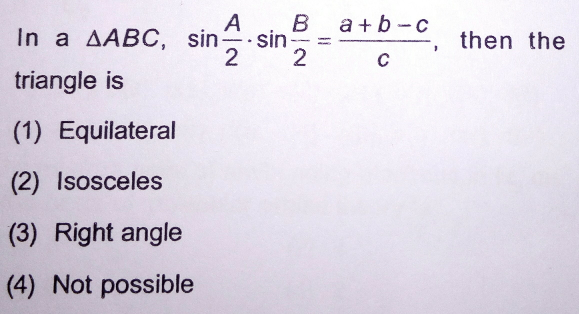
Commented by ajfour last updated on 15/Dec/17
2sin ((A/2))sin ((B/2))=2(((sin A+sin B)/(sin C)))−2 ⇒ cos (((A−B)/2))−cos (((A+B)/2))= ((4sin (((A+B)/2))cos (((A−B)/2)))/(2sin ((C/2))cos ((C/2))))−2 ⇒ as cos ((C/2))=sin (((A+B)/2)) , so [cos (((A−B)/2))−cos (((A+B)/2))]sin (C/2) =2[cos (((A−B)/2))−cos (((A+B)/2))] ⇒ cos (((A−B)/2))−cos (((A+B)/2))=0 or sin Asin B=0 ⇒ Not possible (4) .
$$\mathrm{2sin}\:\left(\frac{{A}}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{{B}}{\mathrm{2}}\right)=\mathrm{2}\left(\frac{\mathrm{sin}\:{A}+\mathrm{sin}\:{B}}{\mathrm{sin}\:{C}}\right)−\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)−\mathrm{cos}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{4sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)}{\mathrm{2sin}\:\left(\frac{{C}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)}−\mathrm{2} \\ $$$$\Rightarrow\:{as}\:\:\:\:\mathrm{cos}\:\left(\frac{{C}}{\mathrm{2}}\right)=\mathrm{sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\:,\:{so} \\ $$$$\left[\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)−\mathrm{cos}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\right]\mathrm{sin}\:\frac{{C}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left[\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)−\mathrm{cos}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\right] \\ $$$$\Rightarrow\:\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)−\mathrm{cos}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${or}\:\:\:\mathrm{sin}\:{A}\mathrm{sin}\:{B}=\mathrm{0} \\ $$$$\Rightarrow\:\:{Not}\:{possible}\:\left(\mathrm{4}\right)\:. \\ $$
Commented by Tinkutara last updated on 16/Dec/17
Thank you Sir!
Answered by behi.8.3.4.17@gmail.com last updated on 15/Dec/17
((a+b)/c)=((sinA+sinB)/(sinC))=((2sin((A+B)/2)cos((A−B)/2))/(2sin(C/2)cos(C/2)))= =((2sin(90−(C/2))cos((A−B)/2))/(2sin(C/2)cos(C/2)))=((cos((A−B)/2))/(sin(C/2))) ⇒sin(A/2)sin(B/2)=((cos((A−B)/2))/(sin(C/2)))−1⇒ Πsin(A/2)=cos((A−B)/2)−cos((A+B)/2)=2sin(A/2)sin(B/2)⇒ ⇒sin(C/2)=2 .■ impossible⇒op.(4) note:sin(C/2)=sin(((180−A−B)/2))=sin(90−((A+B)/2))= =cos((A+B)/2).□
$$\frac{\mathrm{a}+\mathrm{b}}{\mathrm{c}}=\frac{\mathrm{sinA}+\mathrm{sinB}}{\mathrm{sinC}}=\frac{\mathrm{2sin}\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}\mathrm{cos}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}}{\mathrm{2sin}\frac{\mathrm{C}}{\mathrm{2}}\mathrm{cos}\frac{\mathrm{C}}{\mathrm{2}}}= \\ $$$$=\frac{\mathrm{2sin}\left(\mathrm{90}−\frac{\mathrm{C}}{\mathrm{2}}\right)\mathrm{cos}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}}{\mathrm{2sin}\frac{\mathrm{C}}{\mathrm{2}}\mathrm{cos}\frac{\mathrm{C}}{\mathrm{2}}}=\frac{\mathrm{cos}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}}{\mathrm{sin}\frac{\mathrm{C}}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{sin}\frac{\mathrm{A}}{\mathrm{2}}\mathrm{sin}\frac{\mathrm{B}}{\mathrm{2}}=\frac{\mathrm{cos}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}}{\mathrm{sin}\frac{\mathrm{C}}{\mathrm{2}}}−\mathrm{1}\Rightarrow \\ $$$$\Pi\mathrm{sin}\frac{\mathrm{A}}{\mathrm{2}}=\mathrm{cos}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}−\mathrm{cos}\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}=\mathrm{2sin}\frac{\mathrm{A}}{\mathrm{2}}\mathrm{sin}\frac{\mathrm{B}}{\mathrm{2}}\Rightarrow \\ $$$$\Rightarrow\mathrm{sin}\frac{\mathrm{C}}{\mathrm{2}}=\mathrm{2}\:.\blacksquare\:\:\mathrm{impossible}\Rightarrow\mathrm{op}.\left(\mathrm{4}\right) \\ $$$$\mathrm{note}:\mathrm{sin}\frac{\mathrm{C}}{\mathrm{2}}=\mathrm{sin}\left(\frac{\mathrm{180}−\mathrm{A}−\mathrm{B}}{\mathrm{2}}\right)=\mathrm{sin}\left(\mathrm{90}−\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}\right)= \\ $$$$=\mathrm{cos}\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}.\Box \\ $$
Commented by Tinkutara last updated on 16/Dec/17
Thank you Sir!
Answered by behi.8.3.4.17@gmail.com last updated on 15/Dec/17
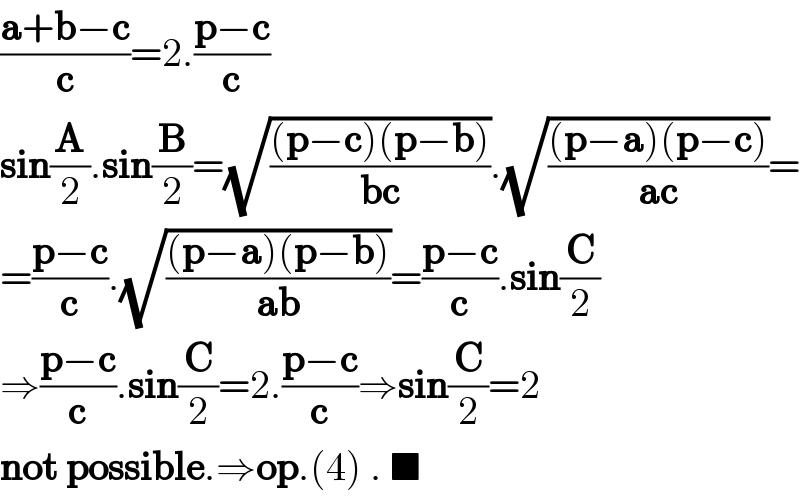
((a+b−c)/c)=2.((p−c)/c) sin(A/2).sin(B/2)=(√(((p−c)(p−b))/(bc))).(√(((p−a)(p−c))/(ac)))= =((p−c)/c).(√(((p−a)(p−b))/(ab)))=((p−c)/c).sin(C/2) ⇒((p−c)/c).sin(C/2)=2.((p−c)/c)⇒sin(C/2)=2 not possible.⇒op.(4) . ■
$$\frac{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}−\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{c}}}=\mathrm{2}.\frac{\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{c}}} \\ $$$$\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{A}}}{\mathrm{2}}.\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{B}}}{\mathrm{2}}=\sqrt{\frac{\left(\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{c}}\right)\left(\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{b}}\right)}{\boldsymbol{\mathrm{bc}}}}.\sqrt{\frac{\left(\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{a}}\right)\left(\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{c}}\right)}{\boldsymbol{\mathrm{ac}}}}= \\ $$$$=\frac{\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{c}}}.\sqrt{\frac{\left(\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{a}}\right)\left(\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{b}}\right)}{\boldsymbol{\mathrm{ab}}}}=\frac{\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{c}}}.\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{c}}}.\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}=\mathrm{2}.\frac{\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{c}}}{\boldsymbol{\mathrm{c}}}\Rightarrow\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{C}}}{\mathrm{2}}=\mathrm{2} \\ $$$$\boldsymbol{\mathrm{not}}\:\boldsymbol{\mathrm{possible}}.\Rightarrow\boldsymbol{\mathrm{op}}.\left(\mathrm{4}\right)\:.\:\blacksquare \\ $$
Commented by Tinkutara last updated on 16/Dec/17
Thank you Sir!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *