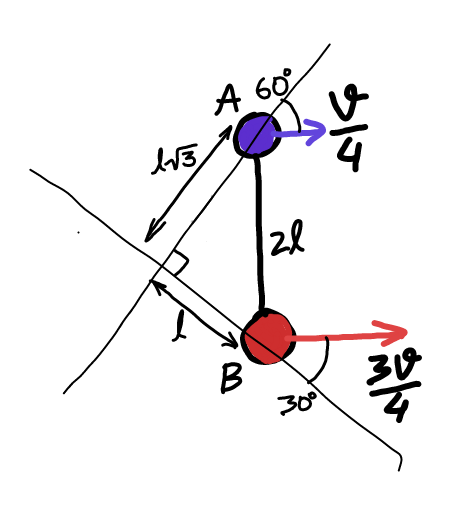
Question Number 25934 by ajfour last updated on 16/Dec/17
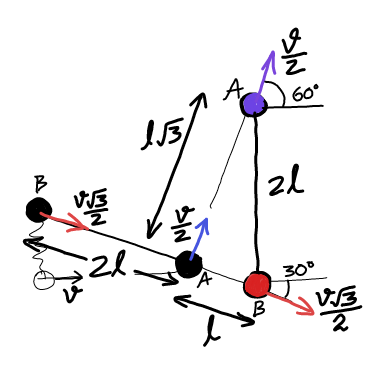
Commented by ajfour last updated on 16/Dec/17
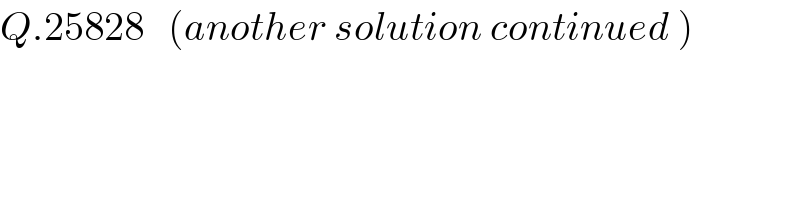
$${Q}.\mathrm{25828}\:\:\:\left({another}\:{solution}\:{continued}\:\right) \\ $$
Commented by ajfour last updated on 16/Dec/17
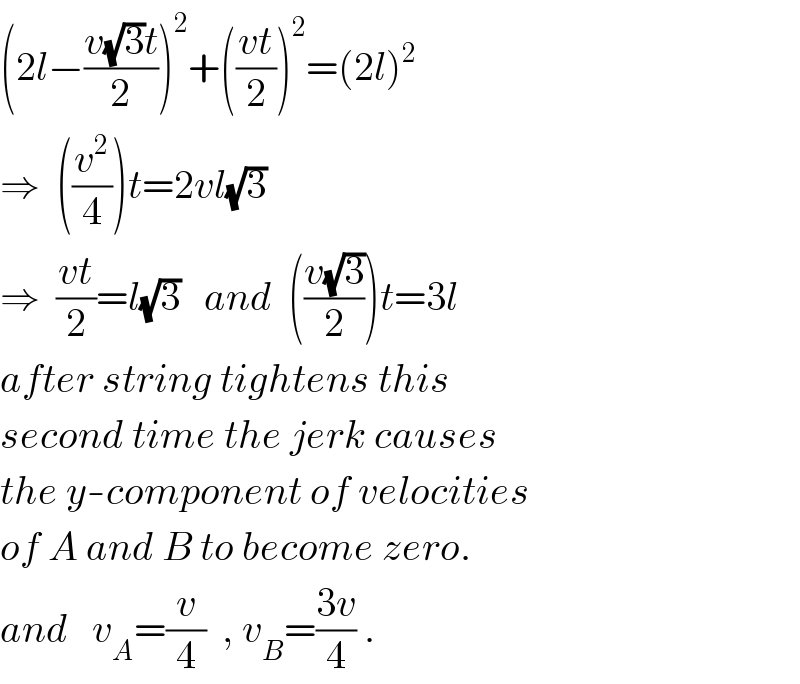
$$\left(\mathrm{2}{l}−\frac{{v}\sqrt{\mathrm{3}}{t}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{vt}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\mathrm{2}{l}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left(\frac{{v}^{\mathrm{2}} }{\mathrm{4}}\right){t}=\mathrm{2}{vl}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\:\frac{{vt}}{\mathrm{2}}={l}\sqrt{\mathrm{3}}\:\:\:{and}\:\:\left(\frac{{v}\sqrt{\mathrm{3}}}{\mathrm{2}}\right){t}=\mathrm{3}{l} \\ $$$${after}\:{string}\:{tightens}\:{this} \\ $$$${second}\:{time}\:{the}\:{jerk}\:{causes} \\ $$$${the}\:{y}-{component}\:{of}\:{velocities} \\ $$$${of}\:{A}\:{and}\:{B}\:{to}\:{become}\:{zero}. \\ $$$${and}\:\:\:{v}_{{A}} =\frac{{v}}{\mathrm{4}}\:\:,\:{v}_{{B}} =\frac{\mathrm{3}{v}}{\mathrm{4}}\:. \\ $$
Answered by ajfour last updated on 16/Dec/17