Question Number 25981 by ifcrna380w last updated on 17/Dec/17
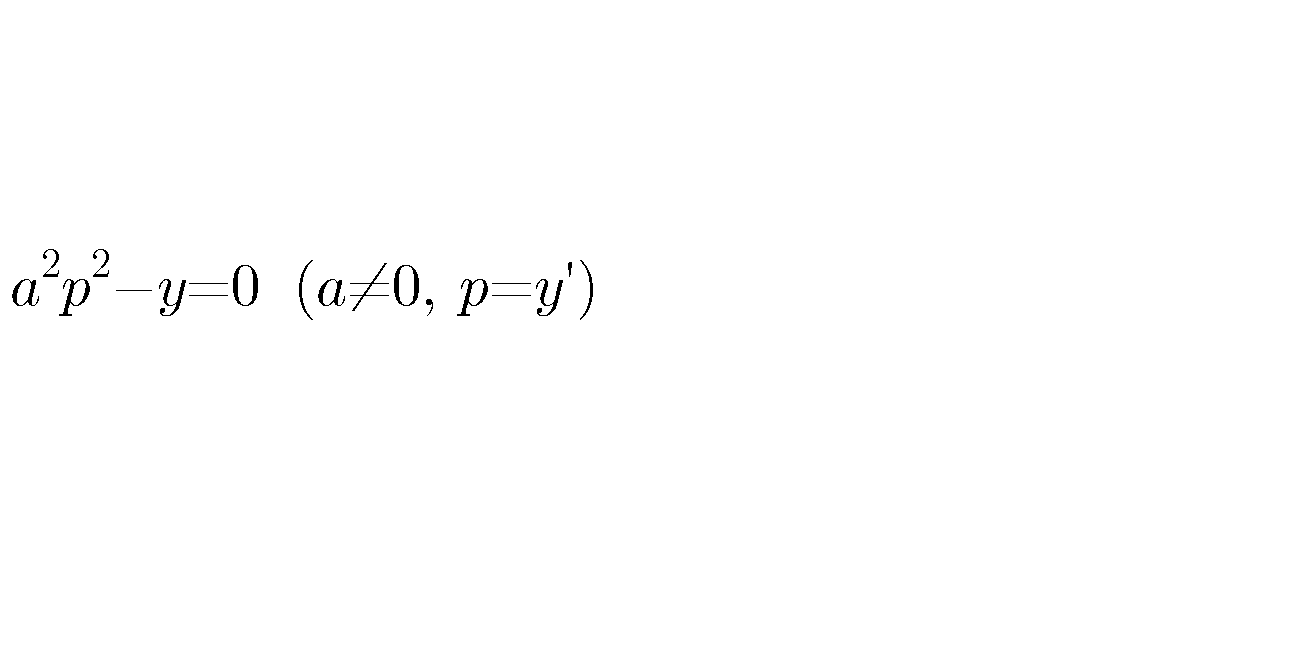
Answered by prakash jain last updated on 17/Dec/17
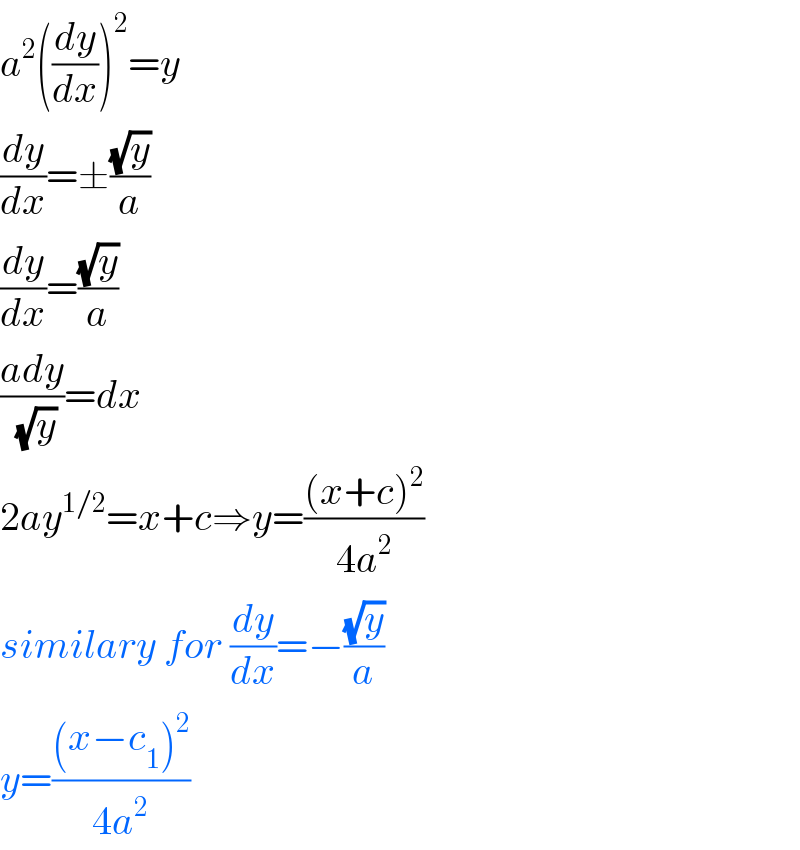
$${a}^{\mathrm{2}} \left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} ={y} \\ $$$$\frac{{dy}}{{dx}}=\pm\frac{\sqrt{{y}}}{{a}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\sqrt{{y}}}{{a}} \\ $$$$\frac{{ady}}{\:\sqrt{{y}}}={dx} \\ $$$$\mathrm{2}{ay}^{\mathrm{1}/\mathrm{2}} ={x}+{c}\Rightarrow{y}=\frac{\left({x}+{c}\right)^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} } \\ $$$${similary}\:{for}\:\frac{{dy}}{{dx}}=−\frac{\sqrt{{y}}}{{a}} \\ $$$${y}=\frac{\left({x}−{c}_{\mathrm{1}} \right)^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} } \\ $$
