Question Number 26125 by offrinshingal last updated on 20/Dec/17
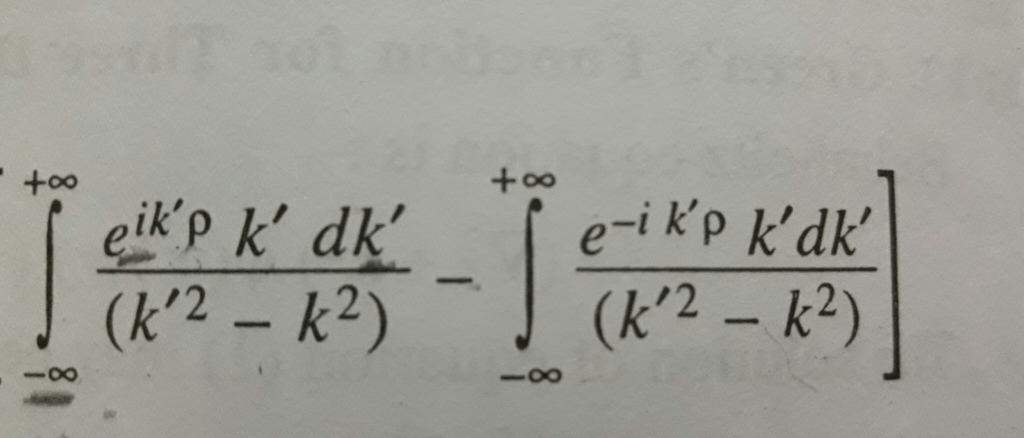
Commented by abdo imad last updated on 21/Dec/17
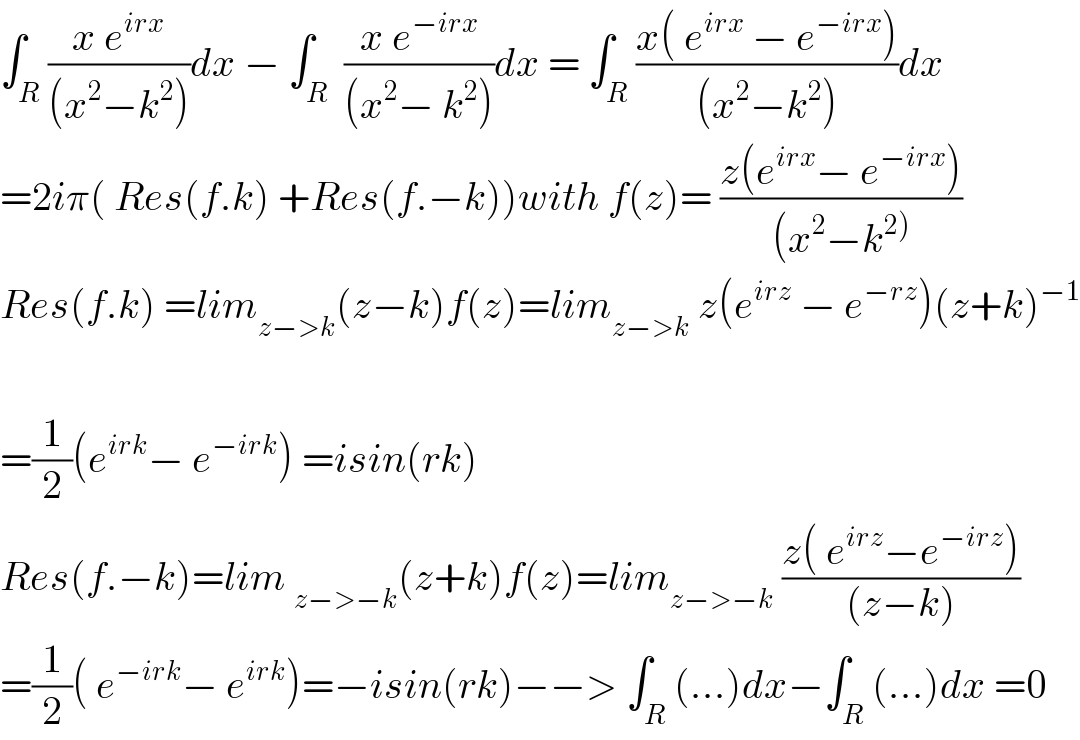
$$\int_{{R}} \frac{{x}\:{e}^{{irx}} }{\left({x}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)}{dx}\:−\:\int_{{R}} \:\frac{{x}\:{e}^{−{irx}} }{\left({x}^{\mathrm{2}} −\:{k}^{\mathrm{2}} \right)}{dx}\:=\:\int_{{R}} \frac{{x}\left(\:{e}^{{irx}} \:−\:{e}^{−{irx}} \right)}{\left({x}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)}{dx} \\ $$$$=\mathrm{2}{i}\pi\left(\:{Res}\left({f}.{k}\right)\:+{Res}\left({f}.−{k}\right)\right){with}\:{f}\left({z}\right)=\:\frac{{z}\left({e}^{{irx}} −\:{e}^{−{irx}} \right)}{\left({x}^{\mathrm{2}} −{k}^{\left.\mathrm{2}\right)} \right.} \\ $$$${Res}\left({f}.{k}\right)\:={lim}_{{z}−>{k}} \left({z}−{k}\right){f}\left({z}\right)={lim}_{{z}−>{k}} \:{z}\left({e}^{{irz}} \:−\:{e}^{−{rz}} \right)\left({z}+{k}\right)^{−\mathrm{1}} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{irk}} −\:{e}^{−{irk}} \right)\:={isin}\left({rk}\right) \\ $$$${Res}\left({f}.−{k}\right)={lim}\:_{{z}−>−{k}} \left({z}+{k}\right){f}\left({z}\right)={lim}_{{z}−>−{k}} \:\frac{{z}\left(\:{e}^{{irz}} −{e}^{−{irz}} \right)}{\left({z}−{k}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\:{e}^{−{irk}} −\:{e}^{{irk}} \right)=−{isin}\left({rk}\right)−−>\:\int_{{R}} \left(…\right){dx}−\int_{{R}} \left(…\right){dx}\:=\mathrm{0} \\ $$
