Question Number 26438 by San Sophanethsan069 last updated on 25/Dec/17

Answered by mrW1 last updated on 25/Dec/17
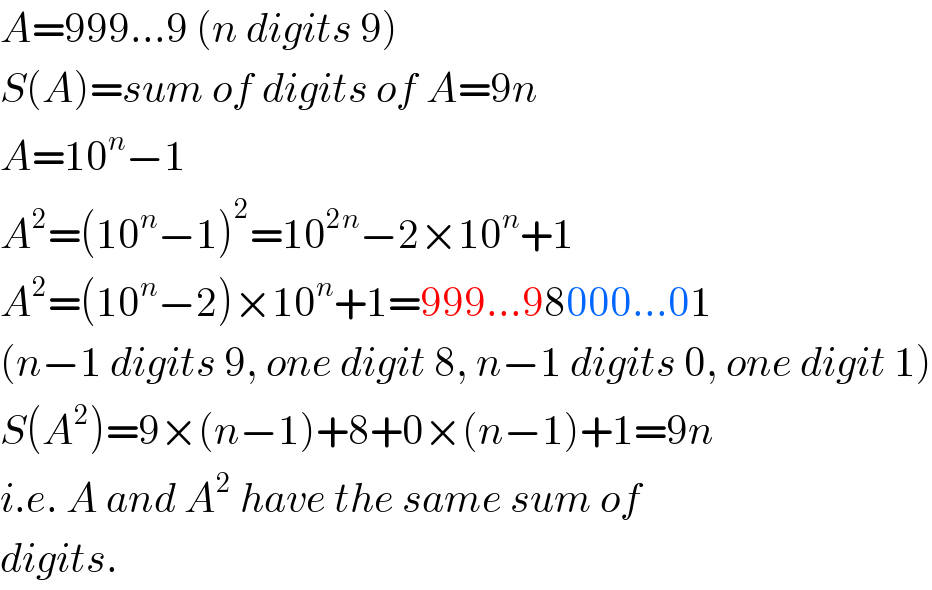
$${A}=\mathrm{999}…\mathrm{9}\:\left({n}\:{digits}\:\mathrm{9}\right) \\ $$$${S}\left({A}\right)={sum}\:{of}\:{digits}\:{of}\:{A}=\mathrm{9}{n} \\ $$$${A}=\mathrm{10}^{{n}} −\mathrm{1} \\ $$$${A}^{\mathrm{2}} =\left(\mathrm{10}^{{n}} −\mathrm{1}\right)^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}{n}} −\mathrm{2}×\mathrm{10}^{{n}} +\mathrm{1} \\ $$$${A}^{\mathrm{2}} =\left(\mathrm{10}^{{n}} −\mathrm{2}\right)×\mathrm{10}^{{n}} +\mathrm{1}=\mathrm{999}…\mathrm{98000}…\mathrm{01} \\ $$$$\left({n}−\mathrm{1}\:{digits}\:\mathrm{9},\:{one}\:{digit}\:\mathrm{8},\:{n}−\mathrm{1}\:{digits}\:\mathrm{0},\:{one}\:{digit}\:\mathrm{1}\right) \\ $$$${S}\left({A}^{\mathrm{2}} \right)=\mathrm{9}×\left({n}−\mathrm{1}\right)+\mathrm{8}+\mathrm{0}×\left({n}−\mathrm{1}\right)+\mathrm{1}=\mathrm{9}{n} \\ $$$${i}.{e}.\:{A}\:{and}\:{A}^{\mathrm{2}} \:{have}\:{the}\:{same}\:{sum}\:{of} \\ $$$${digits}. \\ $$
Commented by San Sophanethsan069 last updated on 26/Dec/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
