Question-26446

Question Number 26446 by yesaditya22@gmail.com last updated on 25/Dec/17

Answered by ajfour last updated on 25/Dec/17

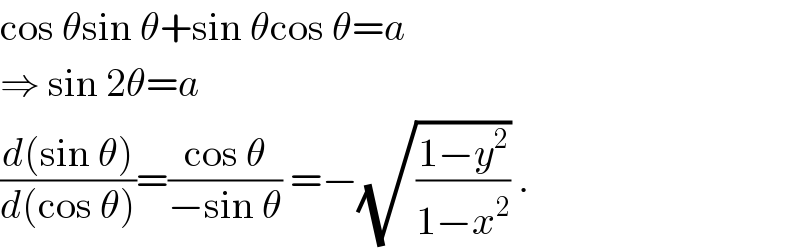
cos θsin θ+sin θcos θ=a ⇒ sin 2θ=a ((d(sin θ))/(d(cos θ)))=((cos θ)/(−sin θ)) =−(√((1−y^2 )/(1−x^2 ))) .

$$\mathrm{cos}\:\theta\mathrm{sin}\:\theta+\mathrm{sin}\:\theta\mathrm{cos}\:\theta={a} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{2}\theta={a} \\ $$$$\frac{{d}\left(\mathrm{sin}\:\theta\right)}{{d}\left(\mathrm{cos}\:\theta\right)}=\frac{\mathrm{cos}\:\theta}{−\mathrm{sin}\:\theta}\:=−\sqrt{\frac{\mathrm{1}−{y}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:. \\ $$

Commented by mrW1 last updated on 26/Dec/17

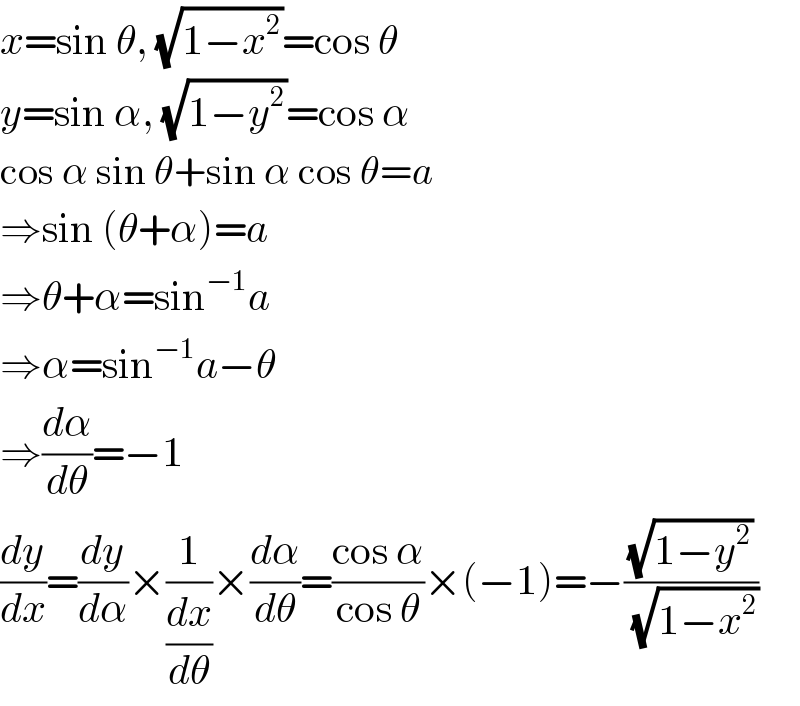
x=sin θ, (√(1−x^2 ))=cos θ y=sin α, (√(1−y^2 ))=cos α cos α sin θ+sin α cos θ=a ⇒sin (θ+α)=a ⇒θ+α=sin^(−1) a ⇒α=sin^(−1) a−θ ⇒(dα/dθ)=−1 (dy/dx)=(dy/dα)×(1/(dx/dθ))×(dα/dθ)=((cos α)/(cos θ))×(−1)=−((√(1−y^2 ))/( (√(1−x^2 ))))

$${x}=\mathrm{sin}\:\theta,\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{cos}\:\theta \\ $$$${y}=\mathrm{sin}\:\alpha,\:\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }=\mathrm{cos}\:\alpha \\ $$$$\mathrm{cos}\:\alpha\:\mathrm{sin}\:\theta+\mathrm{sin}\:\alpha\:\mathrm{cos}\:\theta={a} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\theta+\alpha\right)={a} \\ $$$$\Rightarrow\theta+\alpha=\mathrm{sin}^{−\mathrm{1}} {a} \\ $$$$\Rightarrow\alpha=\mathrm{sin}^{−\mathrm{1}} {a}−\theta \\ $$$$\Rightarrow\frac{{d}\alpha}{{d}\theta}=−\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{d}\alpha}×\frac{\mathrm{1}}{\frac{{dx}}{{d}\theta}}×\frac{{d}\alpha}{{d}\theta}=\frac{\mathrm{cos}\:\alpha}{\mathrm{cos}\:\theta}×\left(−\mathrm{1}\right)=−\frac{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply