Question-26781

Question Number 26781 by shubhabrata04@gmail.com last updated on 29/Dec/17

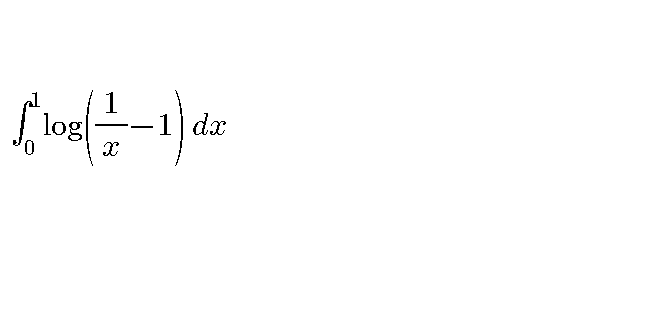
Commented by prakash jain last updated on 29/Dec/17

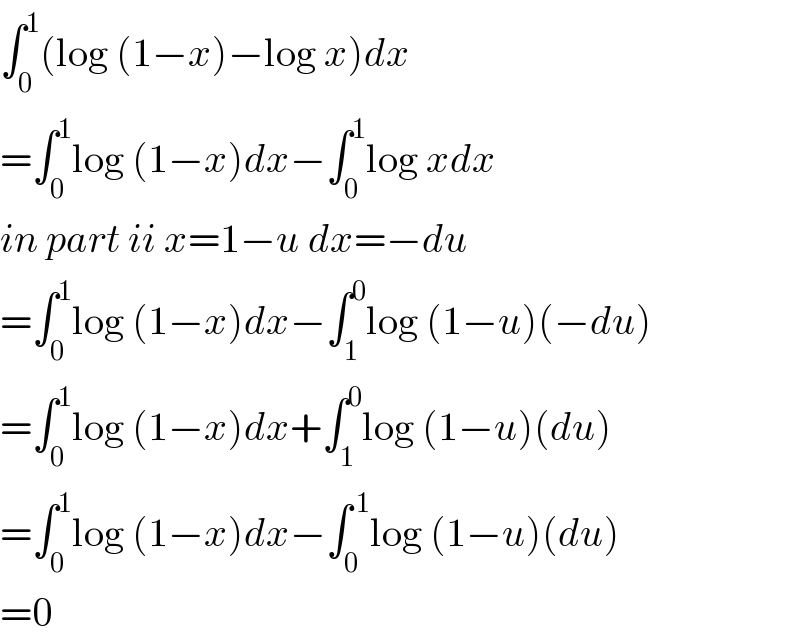
∫_0 ^1 (log (1−x)−log x)dx =∫_0 ^1 log (1−x)dx−∫_0 ^1 log xdx in part ii x=1−u dx=−du =∫_0 ^1 log (1−x)dx−∫_1 ^0 log (1−u)(−du) =∫_0 ^1 log (1−x)dx+∫_1 ^0 log (1−u)(du) =∫_0 ^1 log (1−x)dx−∫_0 ^( 1) log (1−u)(du) =0

$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{log}\:\left(\mathrm{1}−{x}\right)−\mathrm{log}\:{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\:\left(\mathrm{1}−{x}\right){dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\:{xdx} \\ $$$${in}\:{part}\:{ii}\:{x}=\mathrm{1}−{u}\:{dx}=−{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\:\left(\mathrm{1}−{x}\right){dx}−\int_{\mathrm{1}} ^{\mathrm{0}} \mathrm{log}\:\left(\mathrm{1}−{u}\right)\left(−{du}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\:\left(\mathrm{1}−{x}\right){dx}+\int_{\mathrm{1}} ^{\mathrm{0}} \mathrm{log}\:\left(\mathrm{1}−{u}\right)\left({du}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\:\left(\mathrm{1}−{x}\right){dx}−\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{log}\:\left(\mathrm{1}−{u}\right)\left({du}\right) \\ $$$$=\mathrm{0} \\ $$

Commented by malwaan last updated on 29/Dec/17

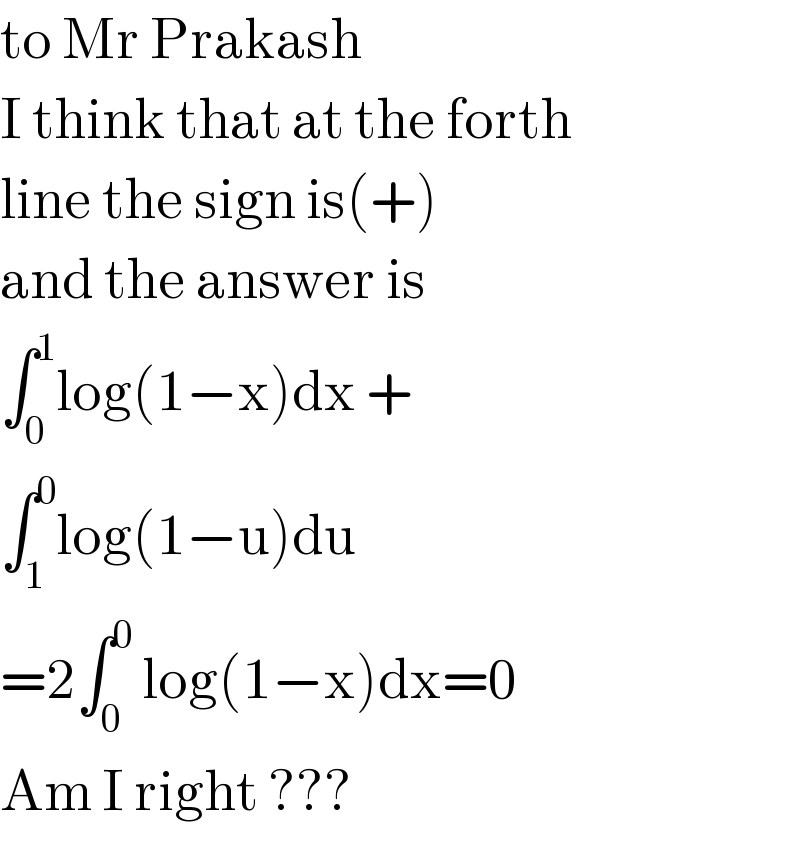
to Mr Prakash I think that at the forth line the sign is(+) and the answer is ∫_0 ^1 log(1−x)dx + ∫_1 ^0 log(1−u)du =2∫_0 ^0 log(1−x)dx=0 Am I right ???

$$\mathrm{to}\:\mathrm{Mr}\:\mathrm{Prakash} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{at}\:\mathrm{the}\:\mathrm{forth}\: \\ $$$$\mathrm{line}\:\mathrm{the}\:\mathrm{sign}\:\mathrm{is}\left(+\right) \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}\:+ \\ $$$$\int_{\mathrm{1}} ^{\mathrm{0}} \mathrm{log}\left(\mathrm{1}−\mathrm{u}\right)\mathrm{du} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{0}} \:\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}=\mathrm{0} \\ $$$$\mathrm{Am}\:\mathrm{I}\:\mathrm{right}\:??? \\ $$

Commented by prakash jain last updated on 29/Dec/17

Yes in the next line I swapped the limits. So we are subtracting same integral. ∫_0 ^1 f(x)dx=−∫_1 ^0 f(x)dx also ∫_0 ^1 f(x)dx+∫_1 ^0 f(x)dx=∫_0 ^0 f(x)dx

$$\mathrm{Yes}\:\mathrm{in}\:\mathrm{the}\:\mathrm{next}\:\mathrm{line}\:\mathrm{I}\:\mathrm{swapped} \\ $$$$\mathrm{the}\:\mathrm{limits}.\:\mathrm{So}\:\mathrm{we}\:\mathrm{are}\:\mathrm{subtracting} \\ $$$$\mathrm{same}\:\mathrm{integral}. \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=−\int_{\mathrm{1}} ^{\mathrm{0}} {f}\left({x}\right){dx} \\ $$$${also} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}+\int_{\mathrm{1}} ^{\mathrm{0}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{0}} {f}\left({x}\right){dx} \\ $$

Commented by malwaan last updated on 31/Dec/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Answered by lee last updated on 29/Dec/17

=∫_0 ^1 {log(1−x)−logx}dx using that ∫logxdx=xlogx−x+c =[−(1−x)log(1−x)+(1−x)]_0 ^1 −[xlogx−x]_0 ^1 =−1+1=0

$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)−\mathrm{logx}\right\}\mathrm{dx} \\ $$$$\mathrm{using}\:\mathrm{that}\:\int\mathrm{logxdx}=\mathrm{xlogx}−\mathrm{x}+\mathrm{c} \\ $$$$=\left[−\left(\mathrm{1}−\mathrm{x}\right)\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)+\left(\mathrm{1}−\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\left[\mathrm{xlogx}−\mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\mathrm{1}+\mathrm{1}=\mathrm{0} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply