Question Number 26824 by kaivan.ahmadi last updated on 30/Dec/17
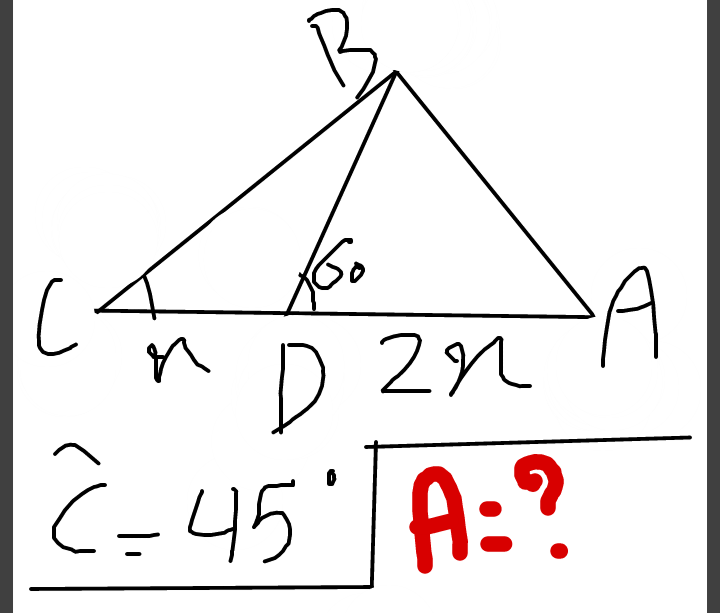
Answered by mrW1 last updated on 30/Dec/17
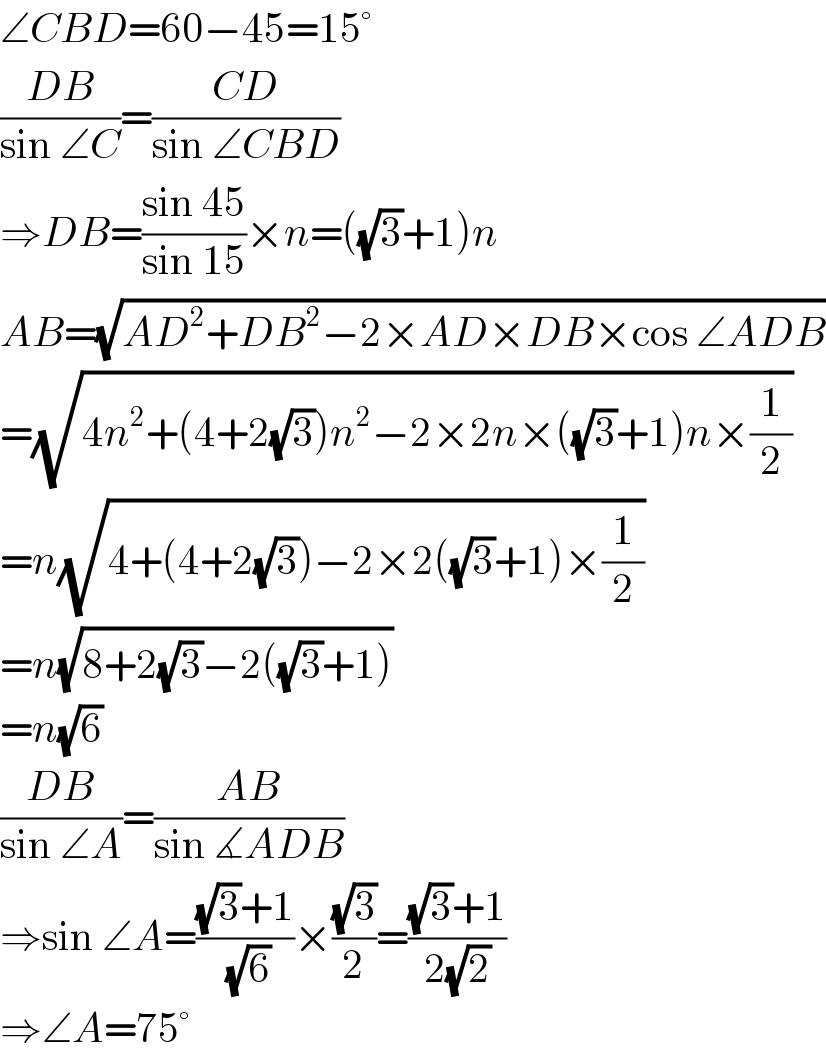
$$\angle{CBD}=\mathrm{60}−\mathrm{45}=\mathrm{15}° \\ $$$$\frac{{DB}}{\mathrm{sin}\:\angle{C}}=\frac{{CD}}{\mathrm{sin}\:\angle{CBD}} \\ $$$$\Rightarrow{DB}=\frac{\mathrm{sin}\:\mathrm{45}}{\mathrm{sin}\:\mathrm{15}}×{n}=\left(\sqrt{\mathrm{3}}+\mathrm{1}\right){n} \\ $$$${AB}=\sqrt{{AD}^{\mathrm{2}} +{DB}^{\mathrm{2}} −\mathrm{2}×{AD}×{DB}×\mathrm{cos}\:\angle{ADB}} \\ $$$$=\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right){n}^{\mathrm{2}} −\mathrm{2}×\mathrm{2}{n}×\left(\sqrt{\mathrm{3}}+\mathrm{1}\right){n}×\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$={n}\sqrt{\mathrm{4}+\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)−\mathrm{2}×\mathrm{2}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)×\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$={n}\sqrt{\mathrm{8}+\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)} \\ $$$$={n}\sqrt{\mathrm{6}} \\ $$$$\frac{{DB}}{\mathrm{sin}\:\angle{A}}=\frac{{AB}}{\mathrm{sin}\:\measuredangle{ADB}} \\ $$$$\Rightarrow\mathrm{sin}\:\angle{A}=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{6}}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\angle{A}=\mathrm{75}° \\ $$
Commented by kaivan.ahmadi last updated on 30/Dec/17

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mrW1 last updated on 30/Dec/17

$${An}\:{other}\:{way}: \\ $$$${let}\:\angle{A}=\alpha \\ $$$$\angle{ABD}=\mathrm{180}−\mathrm{60}−\alpha=\mathrm{120}−\alpha \\ $$$$\frac{{DB}}{\mathrm{sin}\:\alpha}=\frac{\mathrm{2}{n}}{\mathrm{sin}\:\left(\mathrm{120}−\alpha\right)} \\ $$$$\Rightarrow\frac{{n}}{{DB}}=\frac{\mathrm{sin}\:\left(\mathrm{120}−\alpha\right)}{\mathrm{2sin}\:\alpha} \\ $$$$\frac{{DB}}{\mathrm{sin}\:\mathrm{45}}=\frac{{n}}{\mathrm{sin}\:\mathrm{15}} \\ $$$$\Rightarrow\frac{{n}}{{DB}}=\frac{\mathrm{sin}\:\mathrm{15}}{\mathrm{sin}\:\mathrm{45}} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\left(\mathrm{120}−\alpha\right)}{\mathrm{2sin}\:\alpha}=\frac{\mathrm{sin}\:\mathrm{15}}{\mathrm{sin}\:\mathrm{45}} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\left(\mathrm{120}−\alpha\right)}{\mathrm{sin}\:\alpha}=\mathrm{2}×\frac{\mathrm{sin}\:\mathrm{15}}{\mathrm{sin}\:\mathrm{45}}=\mathrm{2}×\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}×\sqrt{\mathrm{2}}=\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\mathrm{120}\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha\:\mathrm{cos}\:\mathrm{120}}{\mathrm{sin}\:\alpha}=\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cot}\:\alpha+\frac{\mathrm{1}}{\mathrm{2}}=\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cot}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}{\:\sqrt{\mathrm{3}}}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\alpha=\mathrm{75}° \\ $$
Answered by ajfour last updated on 30/Dec/17
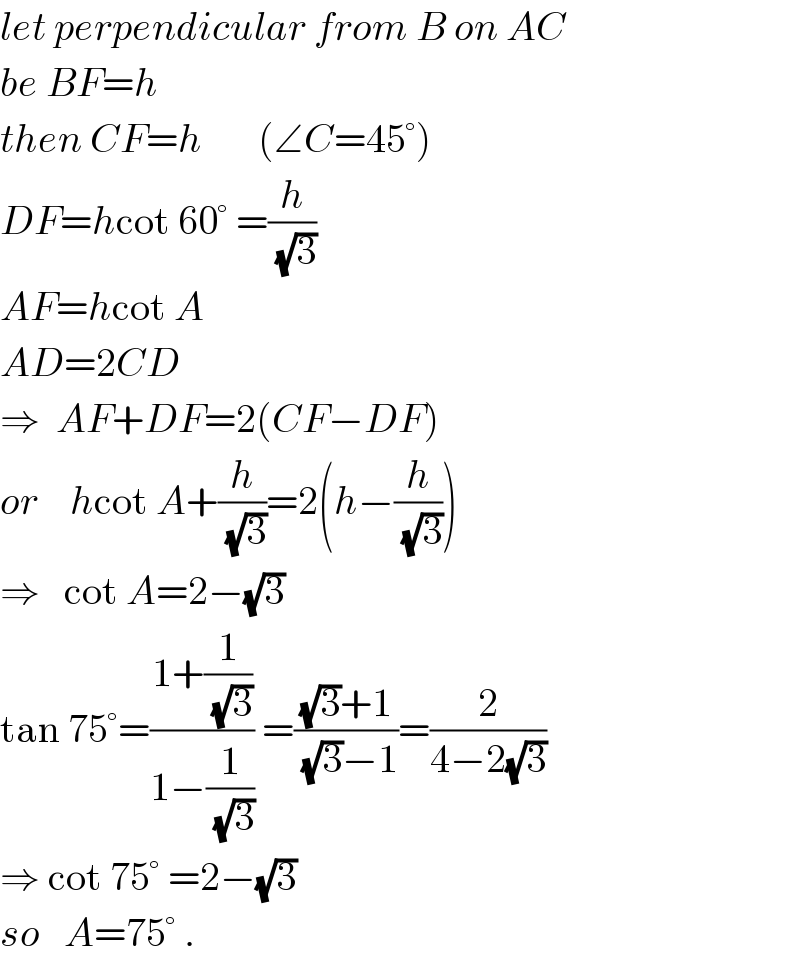
$${let}\:{perpendicular}\:{from}\:{B}\:{on}\:{AC} \\ $$$${be}\:{BF}={h} \\ $$$${then}\:{CF}={h}\:\:\:\:\:\:\:\left(\angle{C}=\mathrm{45}°\right) \\ $$$${DF}={h}\mathrm{cot}\:\mathrm{60}°\:=\frac{{h}}{\:\sqrt{\mathrm{3}}} \\ $$$${AF}={h}\mathrm{cot}\:{A} \\ $$$${AD}=\mathrm{2}{CD} \\ $$$$\Rightarrow\:\:{AF}+{DF}=\mathrm{2}\left({CF}−{DF}\right) \\ $$$${or}\:\:\:\:{h}\mathrm{cot}\:{A}+\frac{{h}}{\:\sqrt{\mathrm{3}}}=\mathrm{2}\left({h}−\frac{{h}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\Rightarrow\:\:\:\mathrm{cot}\:{A}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\mathrm{tan}\:\mathrm{75}°=\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\:=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}−\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:\mathrm{cot}\:\mathrm{75}°\:=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${so}\:\:\:{A}=\mathrm{75}°\:. \\ $$
Commented by mrW1 last updated on 30/Dec/17

$$\mathcal{VERY}\:\mathcal{NICE}! \\ $$
