Menu Close

Question-26853

Tinku Tara 0 Comments
Pin




Question Number 26853 by ajfour last updated on 30/Dec/17
Commented by ajfour last updated on 30/Dec/17
Find area of the blue region.
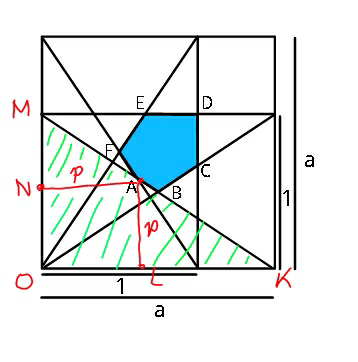
$${Find}\:{area}\:{of}\:{the}\:{blue}\:{region}. \\ $$
Answered by mrW1 last updated on 30/Dec/17
Commented by mrW1 last updated on 31/Dec/17
D(1,1) x_C =1 y_C =(1/a) x_B =(a/2) y_B =(1/2) x_A =y_A (x_A /1)=((a−x_A )/a) ⇒x_A =(a/(1+a))=y_A A_(ABCD) =(1/2)(1−(a/(1+a)))(1+(a/(1+a)))−(1/2)((a/2)−(a/(1+a)))((1/2)+(a/(1+a)))−(1/2)(1−(a/2))((1/2)+(1/a)) A_(Hexagon) =2×A_(ABCD) =(1−(a/(1+a)))(1+(a/(1+a)))−((a/2)−(a/(1+a)))((1/2)+(a/(1+a)))−(1−(a/2))((1/2)+(1/a)) =((1+2a)/((1+a)^2 ))−((a(a−1)(1+3a))/(4(1+a)^2 ))−(((2−a)(2+a))/(4a)) =((4(1+2a)−a(a−1)(1+3a))/(4(1+a)^2 ))−(1/a)+(a/4) =((4+3a^3 +2a^2 +9a)/(4(1+a)^2 ))−(1/a)+(a/4) ......
$${D}\left(\mathrm{1},\mathrm{1}\right) \\ $$$${x}_{{C}} =\mathrm{1} \\ $$$${y}_{{C}} =\frac{\mathrm{1}}{{a}} \\ $$$${x}_{{B}} =\frac{{a}}{\mathrm{2}} \\ $$$${y}_{{B}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}_{{A}} ={y}_{{A}} \\ $$$$\frac{{x}_{{A}} }{\mathrm{1}}=\frac{{a}−{x}_{{A}} }{{a}} \\ $$$$\Rightarrow{x}_{{A}} =\frac{{a}}{\mathrm{1}+{a}}={y}_{{A}} \\ $$$${A}_{{ABCD}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{{a}}{\mathrm{1}+{a}}\right)\left(\mathrm{1}+\frac{{a}}{\mathrm{1}+{a}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{a}}{\mathrm{2}}−\frac{{a}}{\mathrm{1}+{a}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{a}}{\mathrm{1}+{a}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{{a}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{{a}}\right) \\ $$$${A}_{{Hexagon}} =\mathrm{2}×{A}_{{ABCD}} =\left(\mathrm{1}−\frac{{a}}{\mathrm{1}+{a}}\right)\left(\mathrm{1}+\frac{{a}}{\mathrm{1}+{a}}\right)−\left(\frac{{a}}{\mathrm{2}}−\frac{{a}}{\mathrm{1}+{a}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{a}}{\mathrm{1}+{a}}\right)−\left(\mathrm{1}−\frac{{a}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{{a}}\right) \\ $$$$=\frac{\mathrm{1}+\mathrm{2}{a}}{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }−\frac{{a}\left({a}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{3}{a}\right)}{\mathrm{4}\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }−\frac{\left(\mathrm{2}−{a}\right)\left(\mathrm{2}+{a}\right)}{\mathrm{4}{a}} \\ $$$$=\frac{\mathrm{4}\left(\mathrm{1}+\mathrm{2}{a}\right)−{a}\left({a}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{3}{a}\right)}{\mathrm{4}\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{{a}}+\frac{{a}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{4}+\mathrm{3}{a}^{\mathrm{3}} +\mathrm{2}{a}^{\mathrm{2}} +\mathrm{9}{a}}{\mathrm{4}\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{{a}}+\frac{{a}}{\mathrm{4}} \\ $$$$…… \\ $$
Commented by ajfour last updated on 31/Dec/17
thank you Sir, quite enlightening for me.
$${thank}\:{you}\:{Sir},\:{quite}\:{enlightening} \\ $$$${for}\:{me}. \\ $$
Commented by mrW1 last updated on 31/Dec/17
Commented by ajfour last updated on 31/Dec/17
in last line you should have −3a^3 instead of 3a^3 . From your 4^(th) last line Sir, if i expand : A_(hexa) =1−((a/(1+a)))^2 −(a/4)−(a^2 /(2(1+a))) +(a/(2(1+a)))+((a/(1+a)))^2 −(1/2)−(1/a) +(a/4)+(1/2) A_(hexa) =1−((a(a−1))/(2(1+a)))−(1/a) . short enough .
$${in}\:{last}\:{line}\:\:{you}\:{should}\:{have}\:−\mathrm{3}{a}^{\mathrm{3}} \: \\ $$$${instead}\:{of}\:\mathrm{3}{a}^{\mathrm{3}} . \\ $$$${From}\:{your}\:\mathrm{4}^{{th}} \:{last}\:{line}\:{Sir}, \\ $$$${if}\:{i}\:{expand}\:: \\ $$$$\:{A}_{{hexa}} =\mathrm{1}−\left(\frac{{a}}{\mathrm{1}+{a}}\right)^{\mathrm{2}} −\frac{{a}}{\mathrm{4}}−\frac{{a}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+{a}\right)} \\ $$$$\:\:\:\:\:+\frac{{a}}{\mathrm{2}\left(\mathrm{1}+{a}\right)}+\left(\frac{{a}}{\mathrm{1}+{a}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{a}} \\ $$$$\:\:\:\:+\frac{{a}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:{A}_{{hexa}} \:=\mathrm{1}−\frac{{a}\left({a}−\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{1}+{a}\right)}−\frac{\mathrm{1}}{{a}}\:. \\ $$$${short}\:{enough}\:. \\ $$
Commented by ajfour last updated on 31/Dec/17
A_(hexagon) =2[Ar(△OCD)−Ar(△OAB) =2[(1/2)−(1/(2a))−(1/2) determinant (((a/(1+a)),(a/(1+a)),1),((a/2),(1/2),1),(0,0,1))] =1−(1/a)−((a(a−1))/(2(1+a))) .
$${A}_{{hexagon}} =\mathrm{2}\left[{Ar}\left(\bigtriangleup{OCD}\right)−{Ar}\left(\bigtriangleup{OAB}\right)\right. \\ $$$$=\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}{a}}−\frac{\mathrm{1}}{\mathrm{2}}\begin{vmatrix}{\frac{{a}}{\mathrm{1}+{a}}}&{\frac{{a}}{\mathrm{1}+{a}}}&{\mathrm{1}}\\{\frac{{a}}{\mathrm{2}}}&{\frac{\mathrm{1}}{\mathrm{2}}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\end{vmatrix}\right] \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{{a}}−\frac{{a}\left({a}−\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{1}+{a}\right)}\:. \\ $$
Commented by mrW1 last updated on 31/Dec/17
GreaT!
$$\mathcal{G}{rea}\mathcal{T}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *